1.
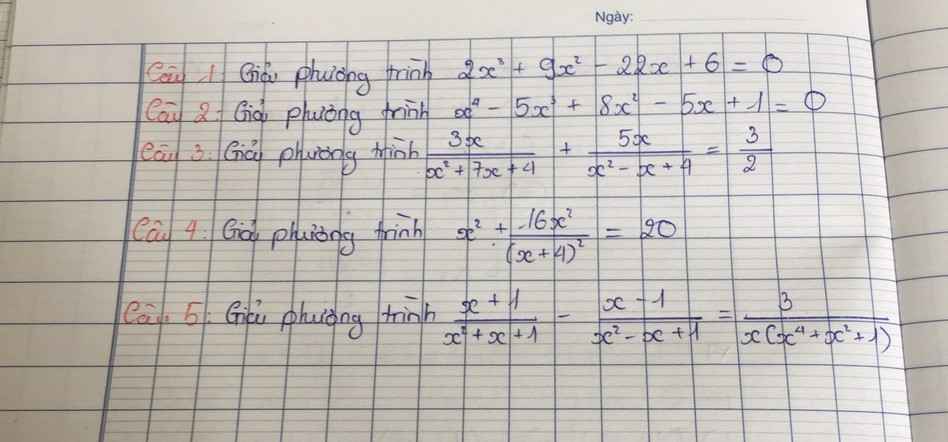
\(2x^3+9x^2-22x+6=0\)
\(\Leftrightarrow2x^3+12x^2-4x-3x^2-18x+6=0\)
\(\Leftrightarrow2x\left(x^2+6x-2\right)-3\left(x^2+6x-2\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(x^2+6x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x^2+6x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-3\pm\sqrt{11}\end{matrix}\right.\)
2.
\(x^4-5x^3+8x^2-5x+1=0\)
Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\) ta được:
\(x^2-5x+8-\dfrac{5}{x}+\dfrac{1}{x^2}=0\)
\(\Leftrightarrow\left(x^2+\dfrac{1}{x^2}+2\right)-5\left(x+\dfrac{1}{x}\right)+6=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2-5\left(x+\dfrac{1}{x}\right)+6=0\)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow t^2-5t+6=0\Rightarrow\left[{}\begin{matrix}t=2\\t=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{x}=2\\x+\dfrac{1}{x}=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-2x+1=0\\x^2-3x+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3\pm\sqrt{5}}{2}\end{matrix}\right.\)
3.
\(\dfrac{3x}{x^2+7x+4}+\dfrac{5x}{x^2-x+4}=\dfrac{3}{2}\)
Nhận thấy \(x=0\) không phải nghiệm, pt tương đương:
\(\dfrac{3}{x+7+\dfrac{4}{x}}+\dfrac{5}{x-1+\dfrac{4}{x}}=\dfrac{3}{2}\)
Đặt \(x-1+\dfrac{4}{x}=t\) pt trở thành:
\(\dfrac{3}{t+8}+\dfrac{5}{t}=\dfrac{3}{2}\)
\(\Rightarrow3t^2+8t-80=0\)
\(\Rightarrow\left[{}\begin{matrix}t=4\\t=-\dfrac{20}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-1+\dfrac{4}{x}=4\\x-1+\dfrac{4}{x}=-\dfrac{20}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-5x+4=0\\3x^2+17x+12=0\end{matrix}\right.\)
\(\Rightarrow...\)
4.
ĐKXĐ: \(x\ne-4\)
\(x^2+\dfrac{16x^2}{\left(x+4\right)^2}=20\)
\(\Leftrightarrow x^2+\left(\dfrac{4x}{x+4}\right)^2-\dfrac{8x^2}{x+4}+\dfrac{8x^2}{x+4}=20\)
\(\Leftrightarrow\left(x-\dfrac{4x}{x+4}\right)^2+\dfrac{8x^2}{x+4}=20\)
\(\Leftrightarrow\left(\dfrac{x^2}{x+4}\right)^2+\dfrac{8x^2}{x+4}-20=0\)
Đặt \(\dfrac{x^2}{x+4}=t\)
\(\Rightarrow t^2+8t-20=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-10\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{x^2}{x+4}=2\\\dfrac{x^2}{x+4}=-10\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-2x-8=0\\x^2+10x+40=0\end{matrix}\right.\)
\(\Rightarrow...\)
5.
ĐKXĐ: \(x\ne0\)
\(\dfrac{x+1}{x^2+x+1}-\dfrac{x-1}{x^2-x+1}=\dfrac{3}{x\left(x^4+x^2+1\right)}\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}-\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{3}{x\left(x^4+x^2+1\right)}\)
\(\Leftrightarrow\dfrac{x^3+1}{x^4+x^2+1}-\dfrac{x^3-1}{x^4+x^2+1}=\dfrac{3}{x\left(x^4+x^2+1\right)}\)
\(\Leftrightarrow\dfrac{3}{x}=2\)
\(\Rightarrow x=\dfrac{3}{2}\)



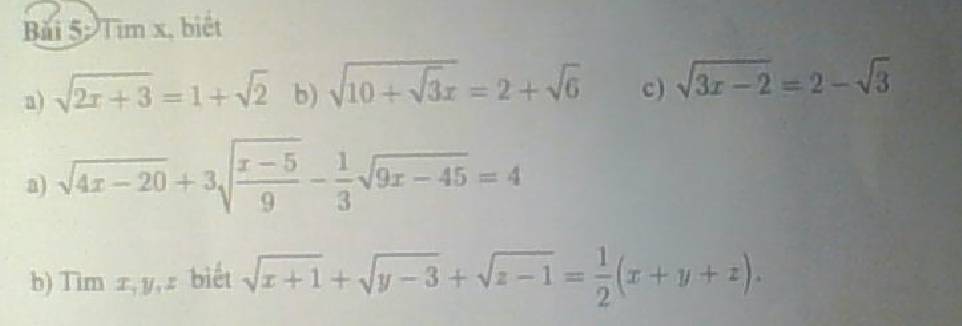


 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.