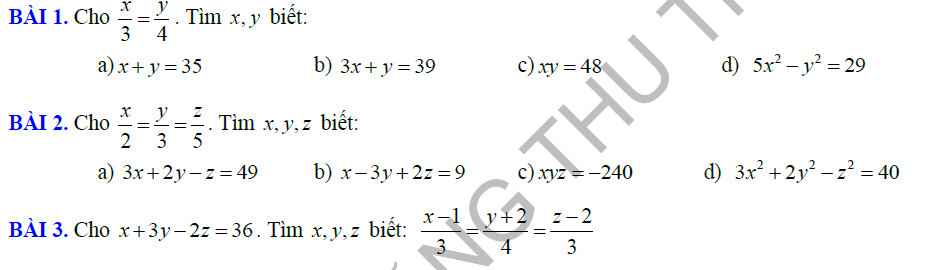Bài 4:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{x+y}{5+6}=\dfrac{44}{11}=4\)
Do đó: x=20; y=24
Bài 1.
a) Áp dụng dãy tỉ số bằng nhau, ta được
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{35}{7}=5\) \(\Rightarrow\left\{{}\begin{matrix}x=15\\y=20\end{matrix}\right.\)
Vậy \(x=15\) và \(y=20\)
b) Áp dụng dãy tỉ số bằng nhau, ta được
\(\dfrac{x}{3}=\dfrac{3x}{9}=\dfrac{y}{4}=\dfrac{3x+y}{9+4}=\dfrac{39}{13}=3\) \(\Rightarrow\left\{{}\begin{matrix}x=9\\y=12\end{matrix}\right.\)
Vậy \(x=9\) và \(y=12\)
c) Ta có \(\left\{{}\begin{matrix}xy=48\\\dfrac{x}{3}=\dfrac{y}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{48}{y}\\3x=4y\end{matrix}\right.\)
\(\Rightarrow4x=3.\dfrac{48}{y}\) \(\Rightarrow x^2=\dfrac{3.48}{4}=36\) \(\Rightarrow x=\pm6\)
Với \(x=6\), ta có \(\dfrac{6}{3}=\dfrac{y}{4}\Rightarrow y=\dfrac{6.4}{3}=8\)
Với \(x=-6\), ta có \(\dfrac{-6}{3}=\dfrac{y}{4}\Rightarrow y=\dfrac{-6.4}{3}=-8\)
Vậy \(\left(x,y\right)\in\left\{\left(6;8\right),\left(-6;-8\right)\right\}\)
Bài 1:
c: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k\\y=4k\end{matrix}\right.\)
Ta có: xy=48
\(\Leftrightarrow12k^2=48\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k=3\cdot2=6\\y=4k=4\cdot2=8\end{matrix}\right.\)
Trường hợp 2: k=-2
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k=3\cdot\left(-2\right)=-6\\y=4k=4\cdot\left(-2\right)=-8\end{matrix}\right.\)