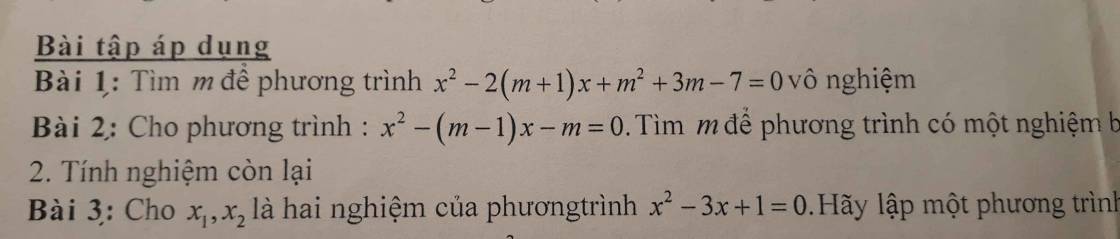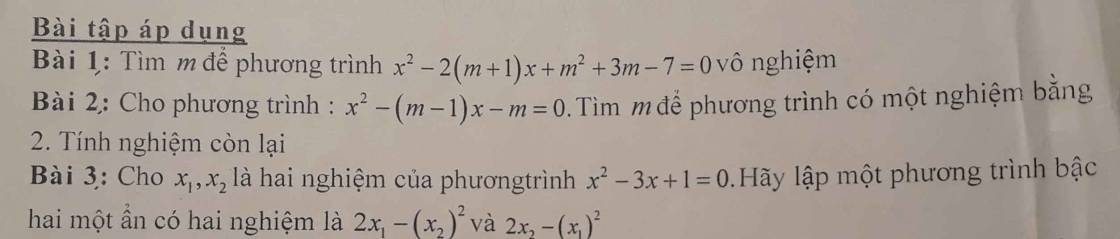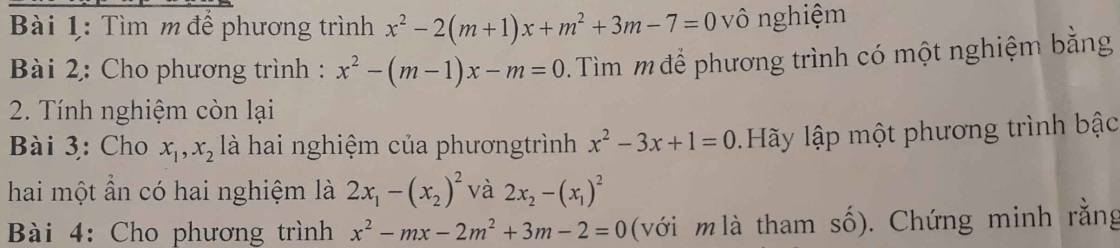ĐKXĐ: \(x>0;x\ne1\)
\(P=\left(\dfrac{2}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\right).\left(\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)}{\sqrt{x}+1}\right)\)
\(=\left(\dfrac{2}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\left(\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)}{\sqrt{x}+1}\right)\)
\(=\left(\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\left(\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)}{\sqrt{x}+1}\right)\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
Bạn tự tìm đkxđ nhé
`P = (2/(x - sqrt x)) + ((sqrt x + 1)(sqrt x -1))/(x - sqrt x) - (x + sqrt x)/(x - sqrt x)) : (sqrtx+1)/(2sqrt x - x)`
`= (2 + x - 1 - x - sqrt x )/(sqrt x(sqrt x - 1)) : (sqrt x + 1)/(2 sqrt x - x)`
`= (-sqrt x + 1)/(sqrt x(sqrt x -1)) : (sqrt x + 1)/(2 sqrt x -x)`
`= (1 - sqrt x)/(sqrt x(sqrt x - 1)) : (sqrt x + 1)/(sqrt x(2 - sqrt x))`
`= -1/sqrt x : (sqrt x + 1)/(sqrt x(2 - sqrt x))`
`= (sqrt x - 2)/(sqrt x + 1)`
mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
