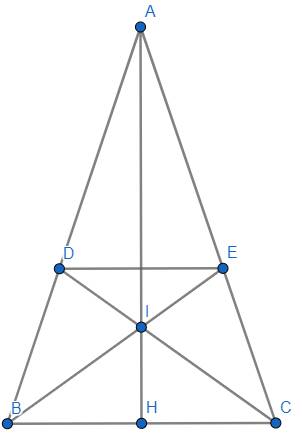
Bài 1. a) Do \(\Delta ABC\) cân tại A (giả thiết) nên \(AB=AC\) và \(\hat{B}=\hat{C}=\dfrac{180^o-\hat{A}}{2}\)
Theo đề bài, \(BD=CE\)
\(\Rightarrow AB-BD=AC-CE\Leftrightarrow AD=AE\).
Suy ra \(\Delta ADE\) cân tại A \(\Rightarrow\hat{D}=\hat{E}=\dfrac{180^o-\hat{A}}{2}\)
Suy ra được : \(\hat{B}=\hat{D}\). Mà hai góc này ở vị trí đồng vị nên \(DE\left|\right|BC\) (điều phải chứng minh).
b) Xét \(\Delta ABE,\Delta ACD\) có : \(\left\{{}\begin{matrix}\hat{A}\text{ chung}\\AD=AE\left(cmt\right)\\AB=AC\left(gt\right)\end{matrix}\right.\Rightarrow\Delta ABE=\Delta ADE\left(c.g.c\right)\)
c) Do \(\Delta ABE=\Delta ACD\left(cmt\right)\) nên \(\hat{DBI}=\hat{ECI}\) (hai góc tương ứng)
Xét các tam giác BID, CIE có : \(\left\{{}\begin{matrix}\hat{DBI}+\hat{DIB}+\hat{BDI}=180^o\\\hat{ECI}+\hat{EIC}+\hat{CIE}=180^o\\\hat{DIB}=\hat{EIC}\left(\text{đối đỉnh}\right);\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{BDI}=\hat{CIE}\).
Lại xét \(\Delta BID,\Delta CIE\) có : \(\left\{{}\begin{matrix}\hat{BDI}=\hat{CIE}\left(cmt\right)\\BD=CE\left(gt\right)\\\hat{DBI}=\hat{ECI}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta BID=\Delta CIE\left(g.c.g\right)\) (điều phải chứng minh).
d) Do \(\Delta BID=\Delta CIE\left(cmt\right)\Rightarrow IB=IC\) (hai cạnh tương ứng).
Xét \(\Delta AIB,\Delta AIC\) có : \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{ABI}=\hat{ACI}\left(cmt\right)\\IB=IC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIB=\Delta AIC\left(c.g.c\right)\Rightarrow\hat{AIB}=\hat{AIC}\)
⇒ \(AI\) là phân giác của \(\hat{BAC}\) (điều phải chứng minh).
e) Gọi \(H\) là giao điểm của \(AI\) và \(BC\).
Xét \(\Delta AHB,\Delta AHC:\) \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\hat{IAB}=\hat{IAC}\left(cmt\right)\\AH\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\Rightarrow\hat{AHB}=\hat{AHC}\).
Mà : \(\hat{AHB}+\hat{AHC}=180^o\) (hai góc kề bù)
\(\Rightarrow\hat{AHB}=\hat{AHC}=\dfrac{180^o}{2}=90^o\Rightarrow AH\perp BC\Rightarrow AI\perp BC\) (điều phải chứng minh).
f) Để \(BD=DE=CE\) thì \(\Delta BDE\) cân tại \(D\) và \(\Delta CDE\) cân tại \(E\).
Xét với tam giác BDE, khi đó : \(\hat{DBE}=\hat{DEB}\).
Mà : \(\hat{DEB}=\hat{EBC}\) (do \(DE\left|\right|BC\left(cmt\right)\) và hai góc ở vị trí so le trong).
\(\Rightarrow\hat{DBE}=\hat{EBC}\) ⇒ BE là đường phân giác của \(\hat{B}\).
Tương tự với tam giác CDE thì CD sẽ là đường phân giác của \(\hat{C}\).
Vậy : \(BD=DE=CE\) khi và chỉ khi D, E lần lượt là giao điểm của đường phân giác tại các đỉnh B, C với AC, AB.
1:
a: AD+DB=AB
AE+EC=AC
mà BD=CE: AB=AC
nên AD=AE
Xet ΔABC có AD/AB=AE/AC
nên DE//BC
b: Xét ΔABE và ΔACD có
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
c: Xet ΔIDB và ΔIEC có
góc IDB=góc IEC
DB=EC
góc IBD=góc ICE
=>ΔIDB=ΔIEC
d: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
=>ΔABI=ΔACI
=>góc BAI=góc CAI
=>AI là phân giác của góc BAC
e: ΔABC cân tại A
mà AI là phân giác
nên AI vuông góc BC