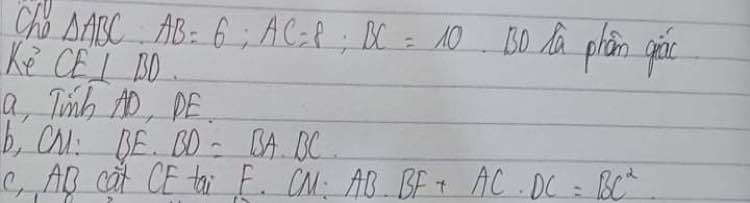a: Xét ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{8}{8}=1\)
Do đó: AD=3cm; CD=5cm
b: Xét ΔBAD vuông tại A và ΔBEC vuông tại E có
\(\widehat{ABD}=\widehat{EBC}\)
Do đó: ΔBAD\(\sim\)ΔBEC
=>BA/BE=BD/BC
hay \(BA\cdot BC=BD\cdot BE\)