a: (3+x^2)^5
SHTQ là: \(C^k_5\cdot\left(x^2\right)^{5-k}\cdot3^k=C^k_5\cdot x^{10-2k}\cdot3^k\)
SỐ hạng chứa x^4 tương ứng với 10-2k=4
=>k=3
=>Số hạng đó là 270x^4
b: \(\Leftrightarrow\dfrac{\left(n+1\right)!}{\left(n+1-1\right)!\cdot1!}+3\cdot\dfrac{\left(n+2\right)!}{\left(n+2-2\right)!\cdot2!}=\dfrac{\left(n+1\right)!}{\left(n+1-3\right)!\cdot3!}\)
=>\(\left(n+1\right)+3\cdot\dfrac{\left(n+1\right)\left(n+2\right)}{2}=\dfrac{\left(n+1\right)\cdot n\cdot\left(n-1\right)}{6}\)
=>6n+6+9(n^2+3n+2)=n^3-n
=>n^3-n=6n+6+9n^2+27n+18=9n^2+33n+24
=>n^3-9n^2-34n-24=0
=>n=12
(x^2+3)^12
SHTQ là \(C^k_{12}\cdot\left(x^2\right)^{12-k}\cdot3^k=C^k_{12}\cdot3^k\cdot x^{24-2k}\)
Số hạng chứa x^6 tương ứng với 24-2k=6
=>2k=18
=>k=9
=>Hệ số là 4330260




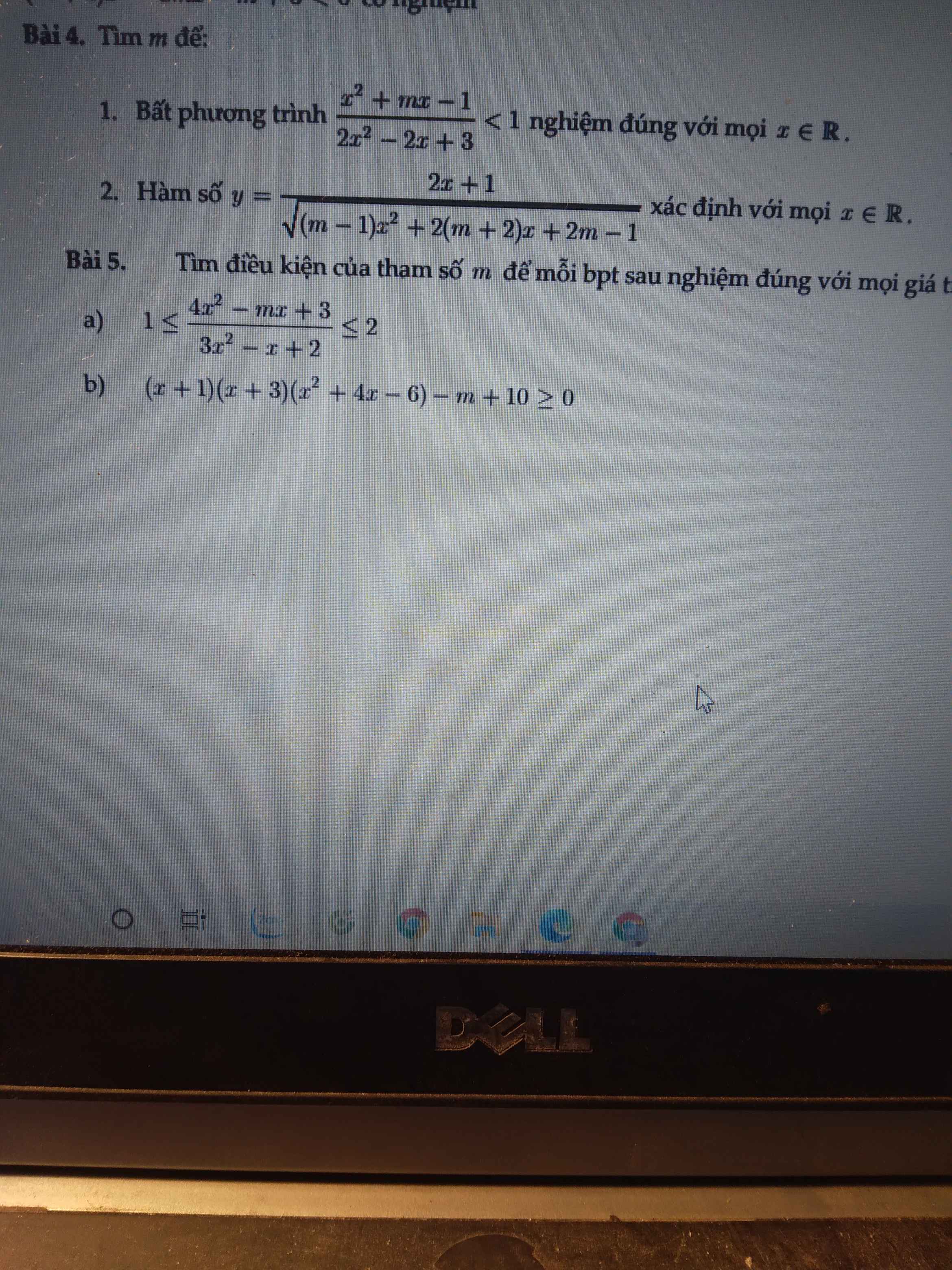
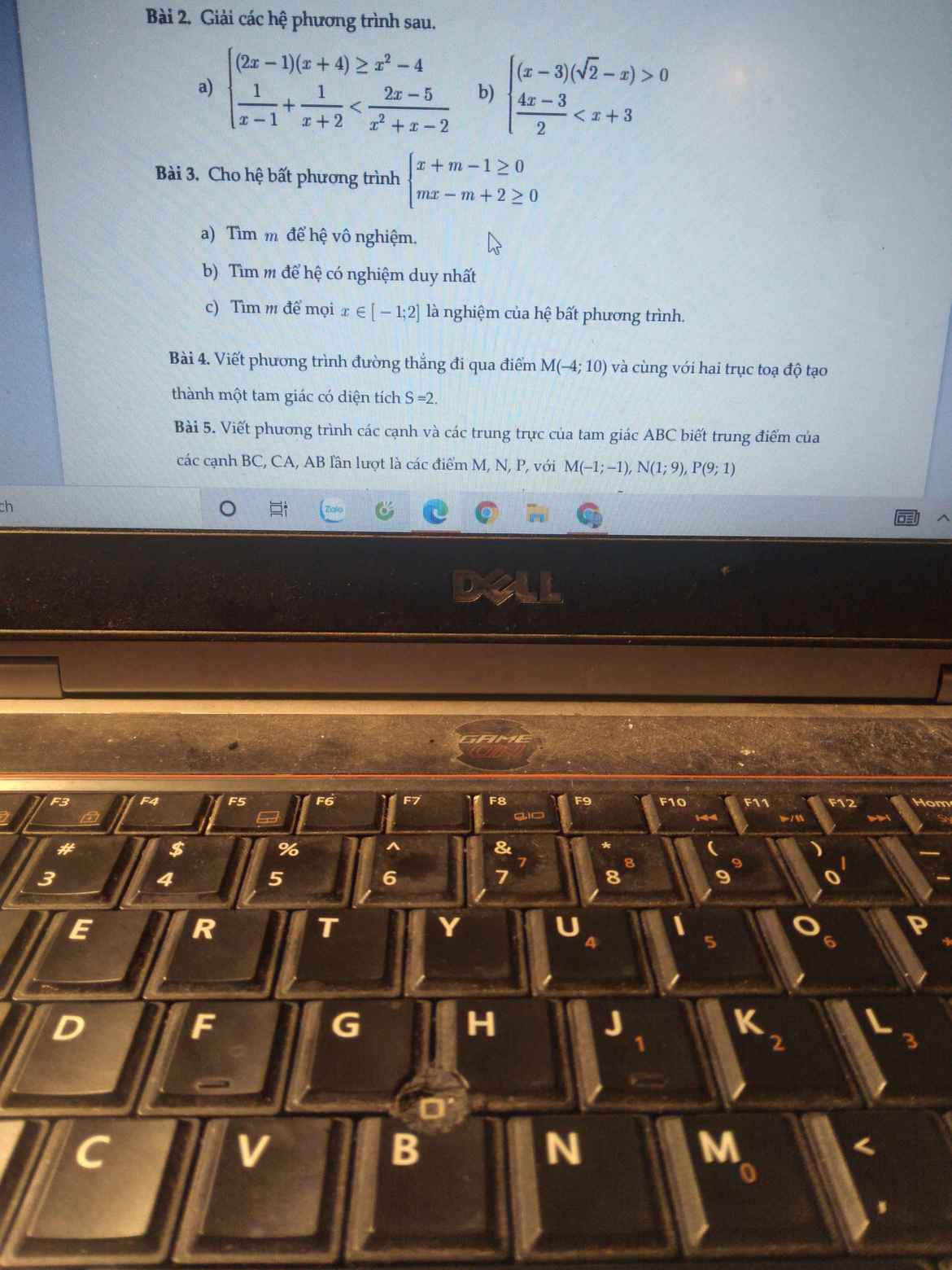



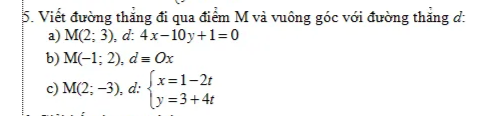
 giúp mình câu b) c) với ạ
giúp mình câu b) c) với ạ