Đáp án B
Mặt phẳng (ABC') chia khối hộp ABCD.A'B'C'D' thành 2 khối lăng trụ BB'C'.AA'D' và BCC'.ADD'
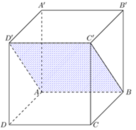
Đáp án B
Mặt phẳng (ABC') chia khối hộp ABCD.A'B'C'D' thành 2 khối lăng trụ BB'C'.AA'D' và BCC'.ADD'

cho khối lăng trụ ABC.A'B'C' gọi M là trung điểm cạnh . Mặt phẳng nào sau đây chia khối lăng trụ ABC.A'B'C' thành hai khối lăng trụ
Cho khối lăng trụ đứng ABCD.A'B'C'D' có đáy là tam giác cân ABC với AB=AC=a, B A C ⏜ = 120 0 mặt phẳng (AB'C') tạo với đáy một góc 30 0 .Tính thể tích V của khối lăng trụ đã cho.
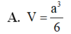
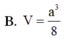
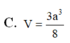
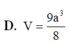
Cho lăng trụ tứ giác đều A B C D . A ' B ' C ' D ' có cạnh đáy bằng 2a. Khoảng cách từ A đến mặt phẳng ( A ' B C ) bằng a 3 . Thể tích khối lăng trụ là.

A. 8 a 3 3
B. 4 a 3 3
C. 8 3 a 3 3
D. 3 a 3 3
Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng 2a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng a 3 . Thể tích khối lăng trụ là.
![]()
![]()
![]()
![]()
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là tam giác ABC vuông cân tại A, cạnh BC=a 6 . Góc giữa mặt phẳng (AB'C) và mặt phẳng (BCC'B') bằng 60 0 . Tính thể tích V của khối đa diện

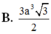
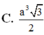
![]()
Cho hình lăng trụ tam giác đều ABC. A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 600, cạnh AB=a. Tính thể tích V của khối lăng trụ ABC. A'B'C'.
A. V = 3 4 a 3
B. V = 3 4 a 3
C. V = 3 3 a 3 8
D. V = 3 a 3
Cho hình lăng trụ đều ABC.A'B'C'. Biết mặt phẳng (A'BC) tạo với mặt phẳng (ABC) một góc 30° và tam giác có A'BC diện tích bằng 8 a 2 . Tính thể tích khối lăng trụ ABC.A'B'C'.
A. 8 3 a 3
B. 8 a 3
C. 8 3 a 3 3
D. 8 a 3 3
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B; AB = a, BC = a 2 ; mặt phẳng (A'BC) hợp với mặt đáy (ABC) góc 30°. Thể tích của khối lăng trụ là:
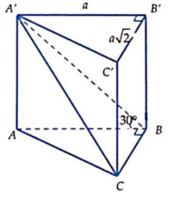
A. a 3 6
B. a 3 6 12
C. a 3 6 3
D. a 3 6 6
Cho hình lăng trụ tam giác đều
ABC.A'B'C' có cạnh đáy bằng a, góc
giữa mặt phẳng (A'BC ) và mặt phẳng
( ABC ) bằng 45o. Thể tích của khối
lăng trụ ABC.A'B'C' bằng
![]()
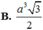
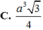
![]()