Câu 25:
2:
a: Xét tứ giác ANME có \(\widehat{ANM}=\widehat{AEM}=\widehat{EAN}=90^0\)
nên ANME là hình chữ nhật
b: Ta có: ME\(\perp\)AC
AB\(\perp\)AC
Do đó; ME//AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét tứ giác AMCD có
E là trung điểm chung của AC và MD
=>AMCD là hình bình hành
Hình bình hành AMCD có AC\(\perp\)MD
nên AMCD là hình thoi
=>AC là phân giác của góc MAD
c: Gọi O là giao điểm của AM và EN
ANME là hình chữ nhật
=>AM=EN
ANME là hình chữ nhật
=>AM cắt NE tại trung điểm của mỗi đường
=>O là trung điểm chung của AM và NE
=>\(AO=OM=\dfrac{AM}{2};EO=ON=\dfrac{EN}{2}\)
mà AM=EN
nên AO=OM=EO=ON=AM/2=EN/2
ΔHAM vuông tại H
mà HO là đường trung tuyến
nên \(HO=\dfrac{AM}{2}=\dfrac{EN}{2}\)
Xét ΔHEN có
HO là đường trung tuyến
HO=EN/2
Do đó: ΔHEN vuông tại H
=>\(\widehat{NHE}=90^0\)





 Vẽ hình giúp mình với nhé cảm ơn nhiều ạ
Vẽ hình giúp mình với nhé cảm ơn nhiều ạ
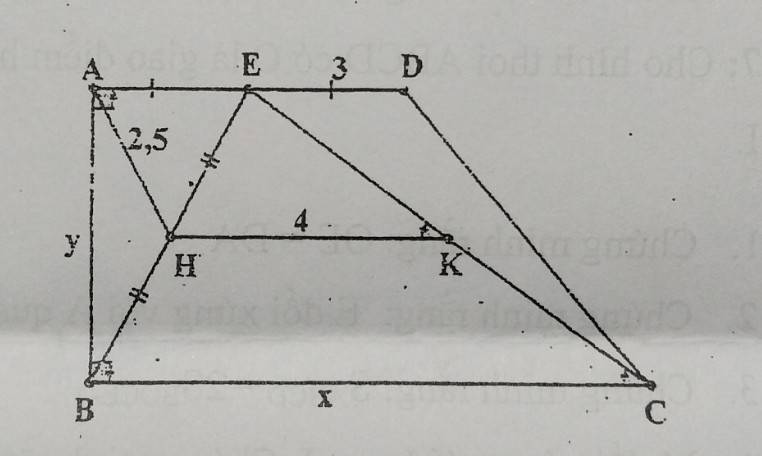
 Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ