1.
Nếu \(a+b+c=0\Rightarrow B=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{\left(-c\right)\left(-a\right)\left(-b\right)}{abc}=-1\)
Theo tính chất dãy tỉ số bằng nhau:
\(\dfrac{a+b-2017c}{c}=\dfrac{b+c-2017a}{a}=\dfrac{c+a-2017b}{b}=\dfrac{a+b-2017c+b+c-2017a+c+a-2017b}{c+a+b}\)
\(=\dfrac{-2015\left(a+b+c\right)}{a+b+c}=-2015\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-2017c=-2015c\\a+c-2017b=-2015b\\b+c-2017a=-2015a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2c-b\\a=2b-c\\b+c=2a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2c-b=2b-c\\b+c=2a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3b=3c\\b+c=2a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=c\\b+c=2a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=c\\b=a\end{matrix}\right.\)
\(\Rightarrow a=b=c\)
Do đó:
\(B=\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)=2.2.2=8\)
2.
Nếu \(a+b+c+d=0\)
\(M=\dfrac{a+b}{c+d}+1+\dfrac{b+c}{d+a}+1+\dfrac{c+d}{a+b}+1+\dfrac{d+a}{b+c}+1-4\)
\(=\dfrac{a+b+c+d}{c+d}+\dfrac{a+b+c+d}{d+a}+\dfrac{a+b+c+d}{a+b}+\dfrac{a+b+c+d}{b+c}-4=-4\)
Nếu \(a+b+c+d\ne0\)
Cộng dãy tỉ số tương tự câu a:
\(\dfrac{2019a+b+c+d}{a}=...=\dfrac{2022\left(a+b+c+d\right)}{a+b+c+d}=2022\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2019a+b+c+d}{a}=2022a\\\dfrac{2019b+a+c+d}{b}=2019b\\\dfrac{2019c+a+b+d}{c}=2019c\\\dfrac{2019d+a+b+c}{d}=2019d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a+b+c=3d\\a+b+d=3c\\a+c+d=3b\\b+c+d=3a\end{matrix}\right.\)
\(\Rightarrow a=b=c=d\)
\(\Rightarrow M=\dfrac{a+a}{a+a}+\dfrac{a+a}{a+a}+\dfrac{a+a}{a+a}+\dfrac{a+a}{a+a}=4\)





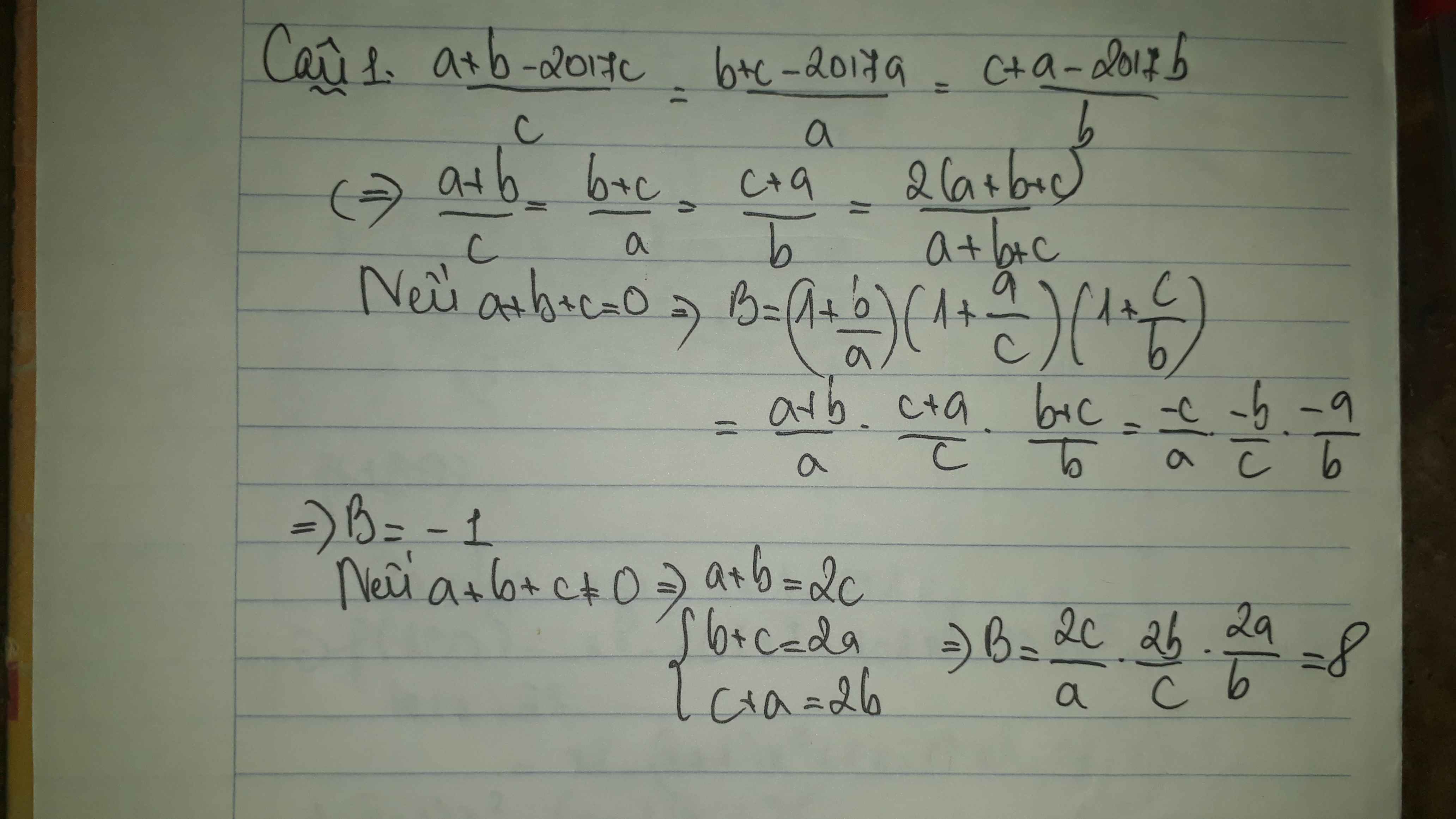

 làm hộ em nhé :>
làm hộ em nhé :>




