5:
a: Giả thiết: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba
Kết luận: Hai đường thẳng đó song song
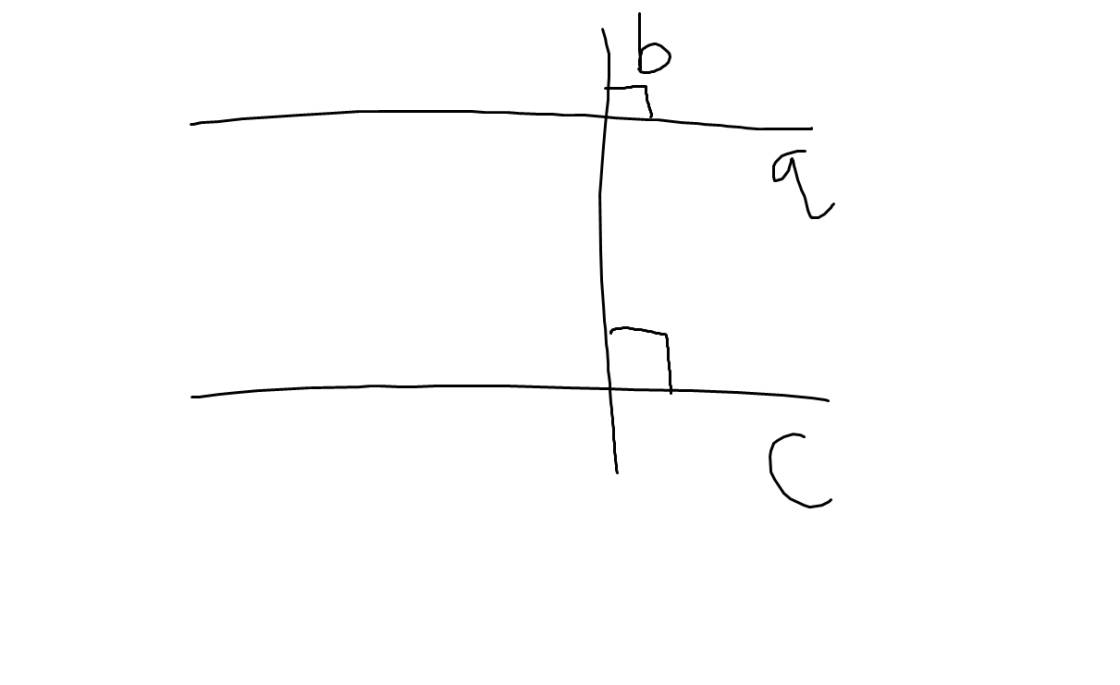
b:
| GT | a\(\perp\)b; b\(\perp\)c |
| KL | a//c |
6:
a: \(\widehat{A_1}\) đồng vị với \(\widehat{B_4}\)
góc A4 là góc so le trong với góc B4
b: \(\widehat{A_2}=\widehat{A_3}\)(hai góc đối đỉnh)
mà \(\widehat{A_3}=140^0\)
nên \(\widehat{A_2}=140^0\)
\(\widehat{A_2}=\widehat{B_3}\)(đồng vị, a//b)
mà \(\widehat{A_2}=140^0\)
nên \(\widehat{B_3}=140^0\)
c: \(\widehat{A_4}=180^0-140^0=40^0\)
ΔBHA vuông tại H
=>\(\widehat{HBA}+\widehat{HAB}=90^0\)
=>\(\widehat{HBA}=90^0-40^0=50^0\)







