\(a,\dfrac{5}{18x^3y}=\dfrac{15y}{54x^3y^2};\dfrac{2}{27x^2y^2}=\dfrac{4x}{54x^3y^2}\\ b,\dfrac{11}{16x^3y^4}=\dfrac{33y}{48x^3y^5};\dfrac{5}{12x^2y^5}=\dfrac{20x}{48x^3y^5}\\ c,\dfrac{5}{3x-12}=\dfrac{10x}{6x\left(x-4\right)};\dfrac{3}{2x^2-8x}=\dfrac{9}{6x\left(x-4\right)}\\ d,\dfrac{2x}{5x^2-5x}=\dfrac{2}{5\left(x-1\right)}=\dfrac{2\left(x+1\right)}{5\left(x-1\right)\left(x+1\right)}\\ \dfrac{x+3}{x^2-1}=\dfrac{5\left(x+3\right)}{5\left(x-1\right)\left(x+1\right)}\\ e,\dfrac{3x+1}{x^2-4}=\dfrac{5\left(3x+1\right)}{5\left(x-2\right)\left(x+2\right)};\dfrac{3}{5x+10}=\dfrac{3\left(x-2\right)}{5\left(x+2\right)\left(x-2\right)}\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
G iúp mình với câu a mình làm rồi ,chỉ làm các câu còn lại hoi
iúp mình với câu a mình làm rồi ,chỉ làm các câu còn lại hoi
Mn giúp mình làm b1 ý4 với làm hết bài 2 với ạ
Làm giúp mình với mình đang cần gấp
Làm giúp mình bài 2,3 với mình cảm ơn
Làm giúp mình với!
Làm giúp mình với
mình cần gấp,làm ơn giúp mình bài 1 với
Đọc tiếp
mình cần gấp,làm ơn giúp mình bài 1 với![]()
![]()
![]()
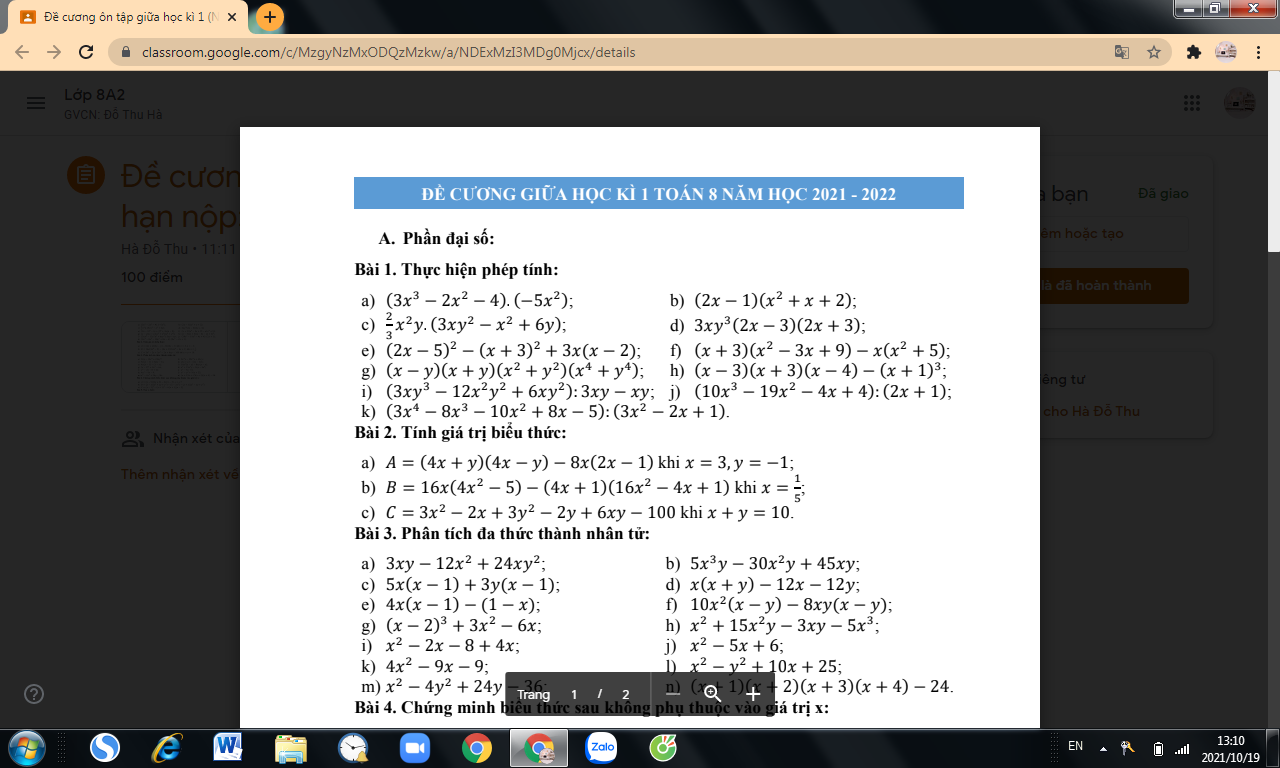
làm cho mình câu 15 16 17 18 giúp mình với
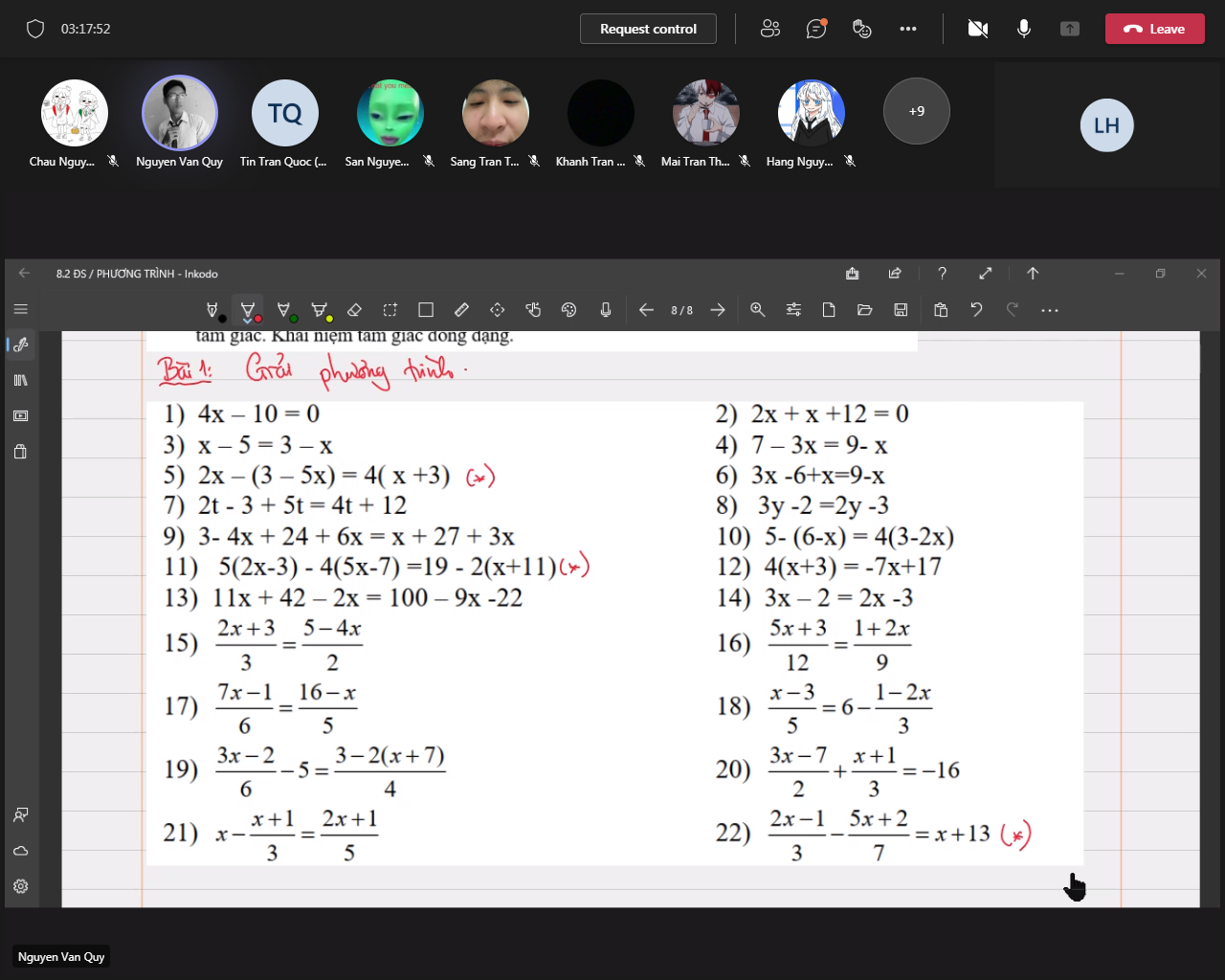
Ai giúp mình làm bài này với ạ, mình cảm ơn nhiều




