Bài 11
Gọi x (học sinh), y (học sinh), z (học sinh), t (học sinh) lần lượt là số học sinh giỏi của khối 6; 7; 8; 9 (x, y, z, t ∈ ℕ*)
Do số học sinh giỏi của khối 6; 7; 8; 9 tỉ lệ với 13; 12; 14; 15 nên ta có:
x/13 = y/12 = z/14 = t/15
Do tổng số hocj sinh giỏi của khối 6; 7 và 8 hơn số học sinh giỏi của khối 9 là 168 em nên:
x + y + z - t = 168
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/13 = y/12 = z/14 = t/15 = (x + y + z - t)/(13 + 12 + 14 - 15) = 168/24 = 7
x/13 = 7 ⇒ x = 7.13 = 91
y/12 = 7 ⇒ y = 7.12 = 84
z/14 = 7 ⇒ z = 7.14 = 98
t/15 = 7 ⇒ t = 7.15 = 105
Vậy số học sinh giỏi của khối 6; 7; 8; 9 lần lượt là: 91 học sinh, 84 học sinh, 98 học sinh, 105 học sinh
Bài 12
Gọi x (học sinh), y (học sinh), z (học sinh) lần lượt là số học sinh cú khối 7; 8 và 9 (x, y, z ∈ ℕ*)
Do số học sinh của khối 6, khối 7, khối 8 lần lượt tỉ lệ với 10; 9; 8 nên ta có:
x/10 = y/9 = z/8
Do số học sinh khối 8 ít hơn số học sinh khối 7 là 50 em nên:
x - y = 50
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/10 = y/9 = z/8 = (x - y)/(10 - 9) = 50/1 = 50
x/10 = 50 ⇒ x = 50.10 = 500
y/9 = 50 ⇒ y = 50.9 = 450
z/8 = 50 ⇒ z = 50.8 = 400
Vậy số học sinh của khối 7, khối 8, khối 9 lần lượt là: 500 học sinh, 450 học sinh, 400 học sinh
Bài 13
Gọi x (học sinh), y (học sinh), z (học sinh) lần lượt là số học sinh giỏi của khối 6; khối 7; khối 8 (x, y, z ∈ ℕ*)
Do số học sinh giỏi của khối 6; khối 7; khối 8 lần lượt tỉ lệ với 5; 4; 3 nên:
x/5 = y/4 = z/3
Do tổng số học sinh giỏi là 480 học sinh nên:
x + y + z = 480
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/5 = y/4 = z/3 = (x + y + z)/(5 + 4 + 3) = 480/12 = 40
x/5 = 40 ⇒ x = 40.5 = 200
y/4 = 40 ⇒ y = 40.4 = 160
z/3 = 40 ⇒ z = 40.3 = 120
Vậy số học sinh giỏi của khối 6, khối 7, khối 8 lần lượt là: 200 học sinh, 160 học sinh, 120 học sinh
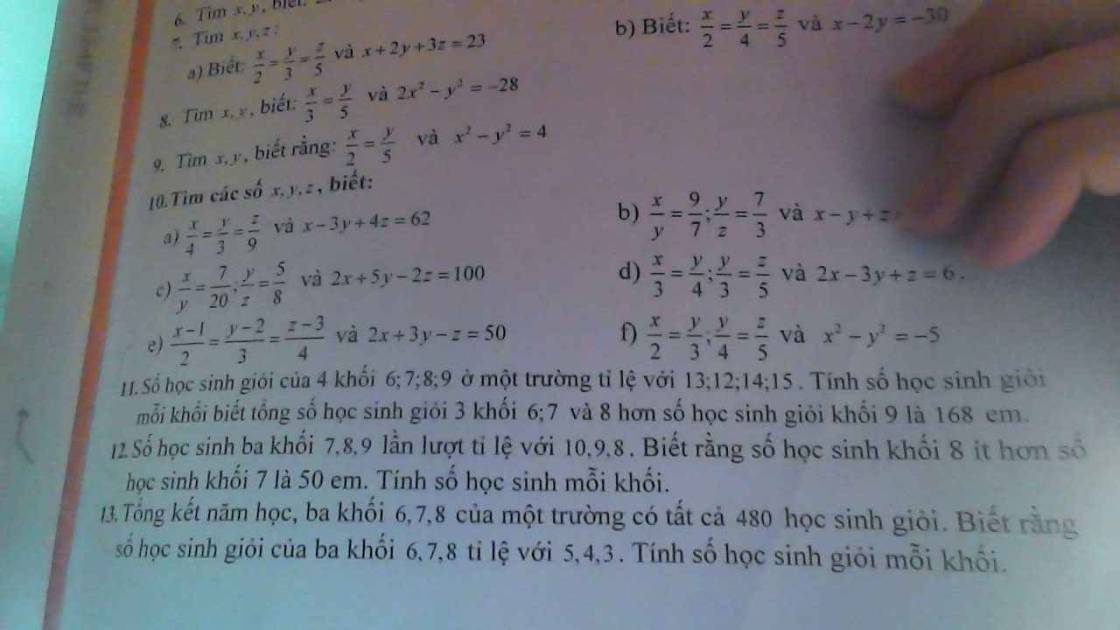





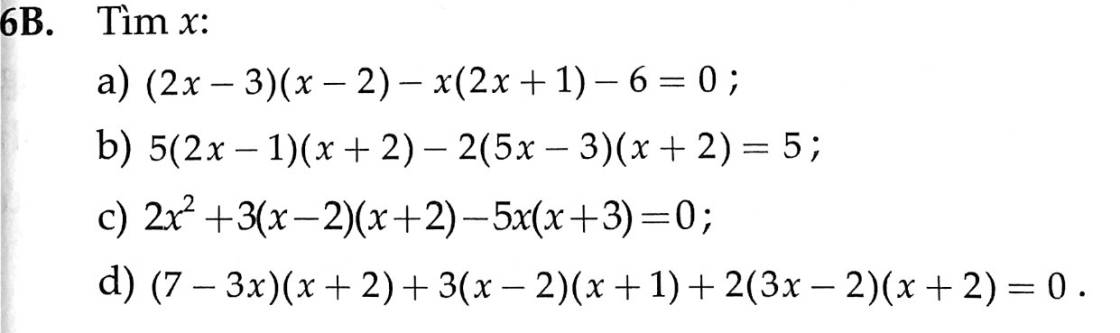
 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ

 giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ
giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ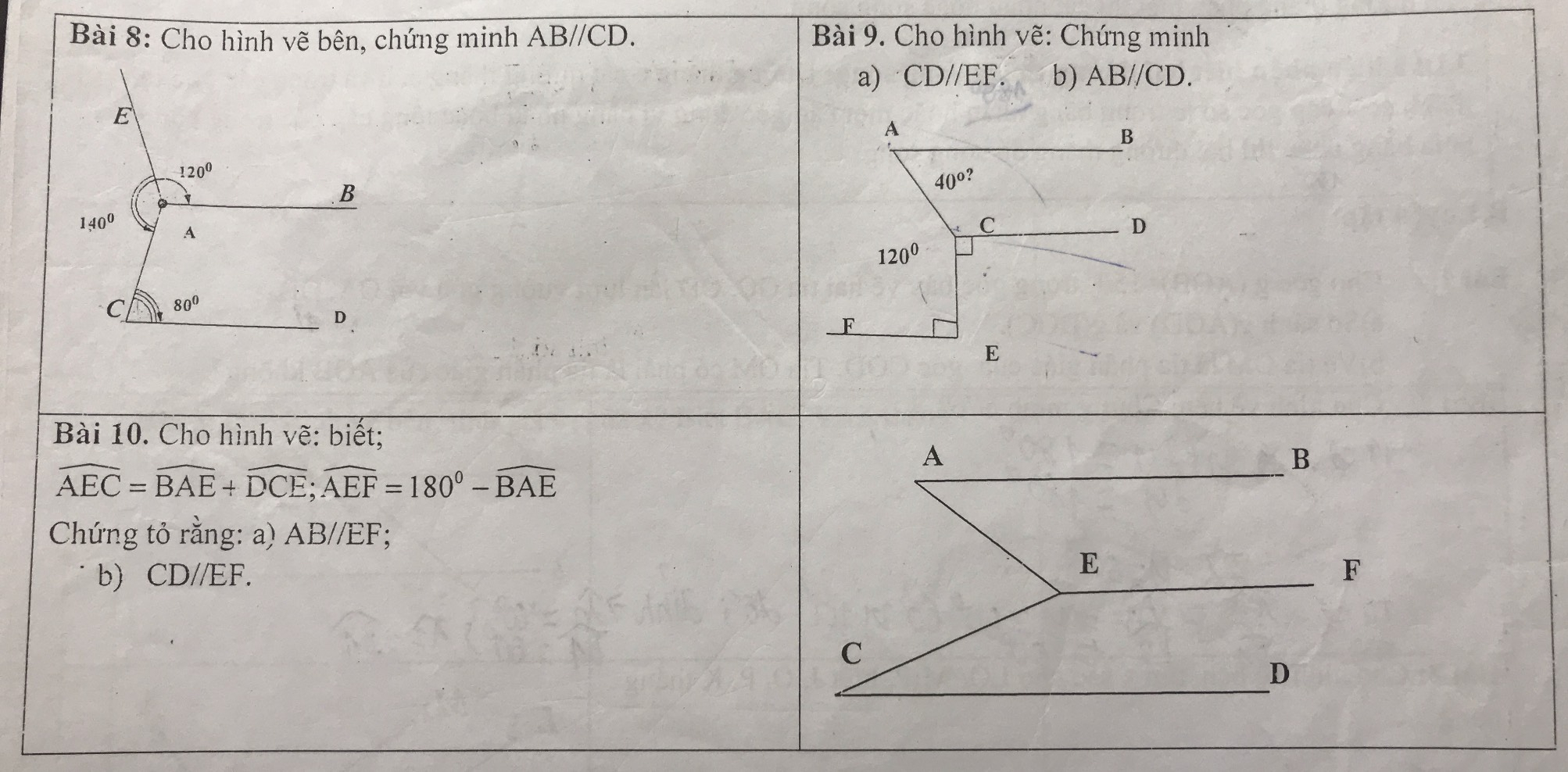 em bài 8,9,10 với ạ em gấp lắm rùi
em bài 8,9,10 với ạ em gấp lắm rùi