3.
Xét \(I=\int\limits^1_0x^3f\left(x^2\right)dx=\int\limits^1_0x^2.f\left(x^2\right)xdx\)
Đặt \(x^2=t\Rightarrow x.dx=\dfrac{1}{2}dt;\) \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=1\Rightarrow t=1\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^1_0t.f\left(t\right).\dfrac{1}{t}dt=\dfrac{1}{2}\int\limits^1_0t.f\left(t\right)dt=3\)
\(\Rightarrow\int\limits^1_0t.f\left(t\right)dt=6\Rightarrow J=\int\limits^1_0x.f\left(x\right)dx=6\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{1}{2}x^2\end{matrix}\right.\)
\(\Rightarrow J=\dfrac{1}{2}x^2.f\left(x\right)|^1_0-\dfrac{1}{2}\int\limits^1_0x^2.f'\left(x\right)dx=2-\dfrac{1}{2}\int\limits^1_0x^2f'\left(x\right)dx=6\)
\(\Rightarrow\int\limits^1_0x^2f'\left(x\right)dx=-8\)
4.
\(I=\int\limits^{\dfrac{\pi}{2}}_0\left(1+cosx+x.cosx\right)e^{sinx}dx=\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx+\int\limits^{\dfrac{\pi}{2}}_0\left(x+1\right)cosx.e^{sinx}dx\)
Xét \(J=\int\limits^{\dfrac{\pi}{2}}_0\left(x+1\right)cosx.e^{sinx}dx\)
Đặt \(\left\{{}\begin{matrix}u=x+1\\dv=cosx.e^{sinx}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^{sinx}\end{matrix}\right.\)
\(\Rightarrow J=\left(x+1\right).e^{sinx}|^{\dfrac{\pi}{2}}_0-\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx=\left(\dfrac{\pi}{2}+1\right)e-1-\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx\)
\(\Rightarrow I=\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx+J=\left(\dfrac{\pi}{2}+1\right)e-1\)
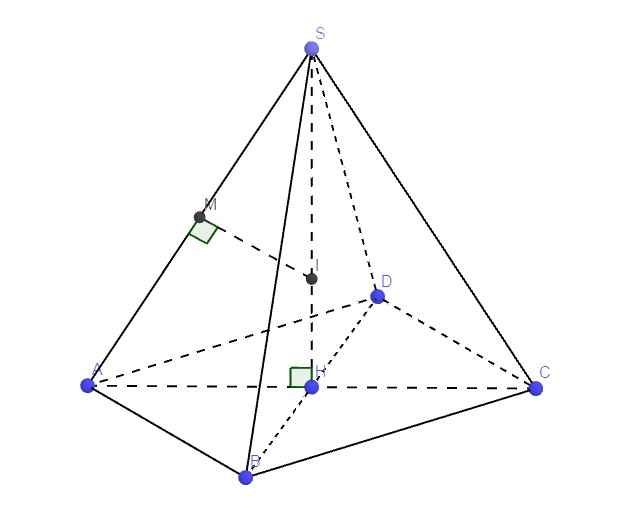
2.
Gọi H là hình chiếu vuông góc của S lên đáy
\(\Rightarrow\widehat{SAH}=\widehat{SBH}=\widehat{SCH}=\widehat{SDH}=60^0\)
\(\Rightarrow SA=SB=SC=SD=\dfrac{SH}{cos60^0}\)
\(\Rightarrow\) Chóp S.ABCD đều và H trùng giao điểm 2 đường chéo AC và BD
Gọi M là trung điểm SA, trong mp (SAH) qua M kẻ đường thẳng vuông góc SA cắt SH tại I
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp
\(AC=\sqrt{AB^2+AD^2}=5\)
\(\Delta SAC\) đều (tam giác cân có 1 góc 60 độ) \(\Rightarrow SA=AC=5\Rightarrow SM=\dfrac{SA}{2}=\dfrac{5}{2}\)
\(\widehat{ASH}=90^0-\widehat{SAH}=30^0\Rightarrow R=SI=\dfrac{SM}{cos30^0}=\dfrac{5\sqrt{3}}{3}\)
\(\Rightarrow V=\dfrac{4}{3}\pi R^3=...\)