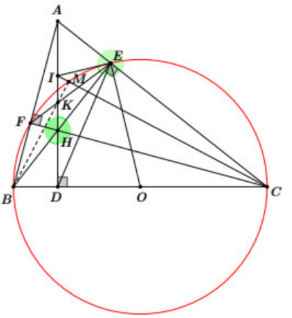
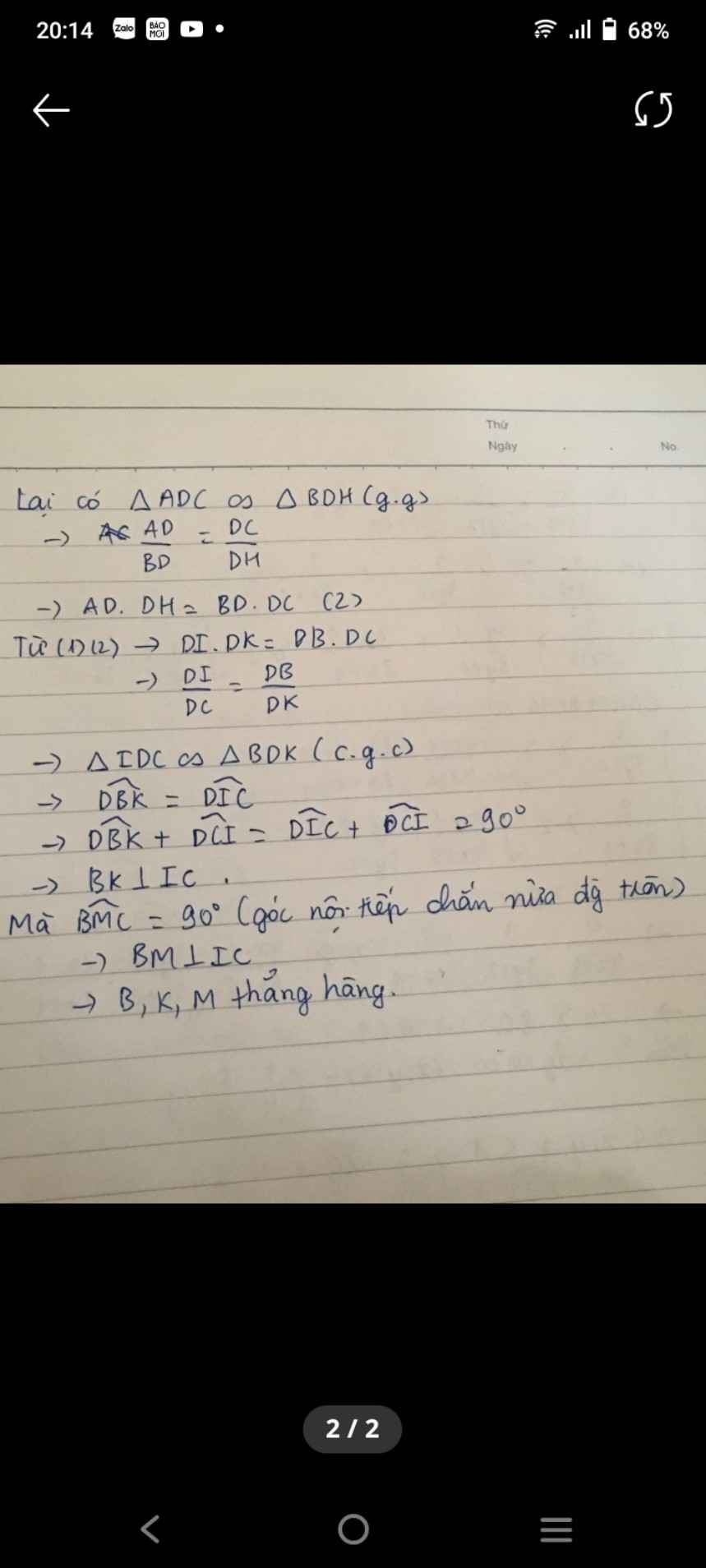Do \(\widehat{ACD}=\widehat{BHD}\) (cùng phụ \(\widehat{DBH}\)) nên 2 tam giác vuông nói trên đồng dạng
Xét tứ giác BADE có :
\(\left\{{}\begin{matrix}\widehat{BDA}=90^o\left(gt\right)\\\widehat{AEB}=90^o\left(gt\right)\end{matrix}\right.\)
mà 2 góc này nằm ở vị trí kề cùng nhìn 1 cạnh
\(\Rightarrow\) TG BADE nội tiếp (O)
Xét \(\Delta ADC\) và \(\Delta BDH\) có :
\(\widehat{ADC}=\widehat{BDH}\left(=90^o\right)\)
\(\widehat{DAC}=\widehat{EBD}\) (cùng chắn \(\stackrel\frown{DE}\) của đtron \(\left(BADE\right)\) )
\(\Rightarrow\Delta ADC\sim\Delta BDH\left(g-g\right)\)