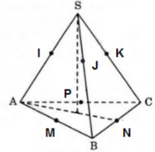
Gọi mặt cầu đã cho có tâm O và bán kính R.
Gọi M, N, P lần lượt là trung điểm của AB, BC và CA.
Gọi I,J và K lần lượt là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu:
+ Từ giả thiết ta suy ra: OI ⊥ SA; OM ⊥ AB
Xét tam giác OIA và tam giác OMA có:
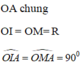
⇒ ∆ OIA = ∆OMA ( ch- cgv)
⇒ AM = AI.
Chứng minh tương tự có: BM= BJ và SI = SJ (1)
Mà AM = BM nên AI= BJ ; (2)
Từ (1) và (2) suy ra: SI+IA = SJ + BJ hay SA = SB (3)
* Chứng minh tương tự, ta có SB= SC (4).
Từ (3) và (4) suy ra: SA = SB = SC (*)
Mặt khác ; BM = BN (= BJ) và CN = CP (= CK)
Suy ra; AB = 2BM = BC = 2 CN = 2CP = CA
Do đó, tam giác ABC là tam giác đều (**)
Từ (*) và (**) suy ra, S. ABC là hình chóp tam giác đều.