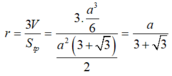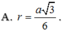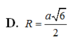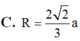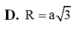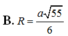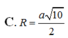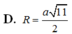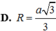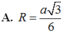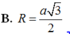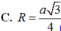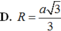Đáp án là A
Cách 1. Áp dụng công thức: r = 3 V S t p (*) và tam giác đều cạnh x có diện tích S = x 2 3 4 .
Từ giả thiết S.ABC đều có SA=SB=SC. Lại có SA, SB, SC đôi một vuông góc và thể tích khối chóp S.ABC bằng a 3 6 nên ta có SA=SB=SC=a.
Suy ra AB=BC=CA=a 2 và tam giác ABC đều cạnh có độ dài a 2 . Do đó diện tích toàn phần của khối chóp S.ABC là
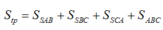
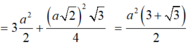
Thay vào (*) ta được: