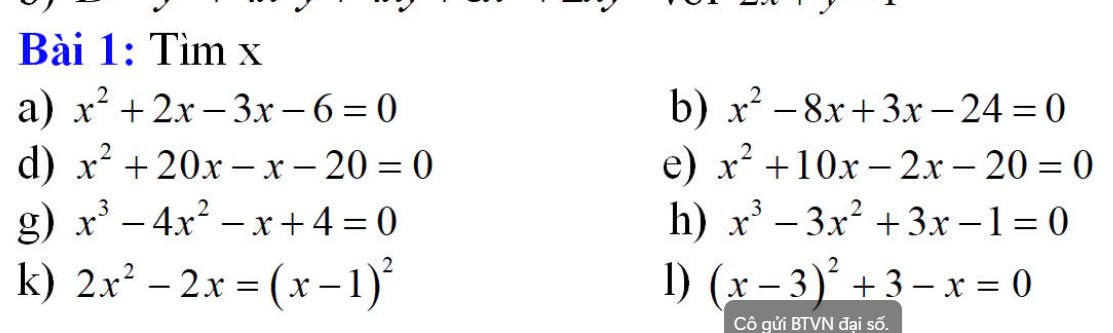a: \(x^2+2x-3x-6=0\)
=>x(x+2)-3(x+2)=0
=>(x+2)(x-3)=0
=>\(\left[{}\begin{matrix}x+2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)
d: \(x^2+20x-x-20=0\)
=>x(x+20)-(x+20)=0
=>(x+20)(x-1)=0
=>\(\left[{}\begin{matrix}x+20=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-20\\x=1\end{matrix}\right.\)
g: \(x^3-4x^2-x+4=0\)
=>\(x^2\left(x-4\right)-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(x^2-1\right)=0\)
=>(x-4)(x+1)(x-1)=0
=>\(\left[{}\begin{matrix}x-4=0\\x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-1\\x=1\end{matrix}\right.\)
k: \(2x^2-2x=\left(x-1\right)^2\)
=>\(2x\left(x-1\right)=\left(x-1\right)^2\)
=>\(2x\left(x-1\right)-\left(x-1\right)^2=0\)
=>\(\left(x-1\right)\left(2x-x+1\right)=0\)
=>(x-1)(x+1)=0
=>\(\left[{}\begin{matrix}x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
b: \(x^2-8x+3x-24=0\)
=>x(x-8)+3(x-8)=0
=>(x-8)(x+3)=0
=>\(\left[{}\begin{matrix}x-8=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-3\end{matrix}\right.\)
e: \(x^2+10x-2x-20=0\)
=>x(x+10)-2(x+10)=0
=>(x+10)(x-2)=0
=>\(\left[{}\begin{matrix}x+10=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-10\\x=2\end{matrix}\right.\)
h: \(x^3-3x^2+3x-1=0\)
=>\(x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3=0\)
=>\(\left(x-1\right)^3=0\)
=>x-1=0
=>x=1
l: \(\left(x-3\right)^2+3-x=0\)
=>\(\left(x-3\right)^2-\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(x-3-1\right)=0\)
=>\(\left(x-3\right)\left(x-4\right)=0\)
=>\(\left[{}\begin{matrix}x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)