Áp dụng BĐT Bunhiacopxki (cho tất cả các bài):
1.
\(\left(3x+4y\right)^2\le\left(3^2+4^2\right)\left(x^2+y^2\right)=25\)
\(\Rightarrow\left|3x+4y\right|\le5\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)
2.
\(\left(x+2y\right)^2=\left(1.x+\sqrt{2}.\sqrt{2y}\right)^2\le\left(1+2\right)\left(x^2+2y^2\right)=3\)
\(\Rightarrow\left|x+2y\right|\le\sqrt{3}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{\sqrt{3}};\dfrac{1}{\sqrt{3}}\right)\)
4.
a.
Áp dụng Bunhiacopxki:
\(\left(b+c+c+a+a+b\right)\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow2\left(a+b+c\right)\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{a+b+c}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)
3.
Từ giả thiết:
\(x^2+y^2+z^2-2x-4y+2z=3\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2=9\)
Ta có:
\(\left|x+2y+2z-20\right|=\left|x-1+2\left(y-2\right)+2\left(z+1\right)-17\right|\)
\(\Rightarrow\left|x+2y+2z-20\right|\le\left|x-1+2\left(y-2\right)+2\left(z+1\right)\right|+17\)
Lại có:
\(\left[\left(x-1\right)+2\left(y-2\right)+2\left(z+1\right)\right]^2\le\left(1+4+4\right)\left[\left(x-1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2\right]=81\)
\(\Rightarrow\left|x-1+2\left(y-2\right)+2\left(z+1\right)\right|\le9\)
\(\Rightarrow\left|x+2y+2z-20\right|\le9+17=26\)
\(\Rightarrow A_{max}=26\) khi \(\left(x;y;z\right)=\left(0;0;-3\right)\)
4b.
\(2\left(ab+bc+ca\right)\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(=\left(ab+ac+bc+ab+ac+bc\right)\left(\dfrac{a^2}{ab+ac}+\dfrac{b^2}{bc+ab}+\dfrac{c^2}{ac+bc}\right)\)
\(\ge\left(\sqrt{ab+ac}.\sqrt{\dfrac{a^2}{ab+ac}}+\sqrt{bc+ab}.\sqrt{\dfrac{b^2}{bc+ab}}+\sqrt{ac+bc}.\sqrt{\dfrac{c^2}{ac+bc}}\right)^2\)
\(=\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)
\(\Rightarrow\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)
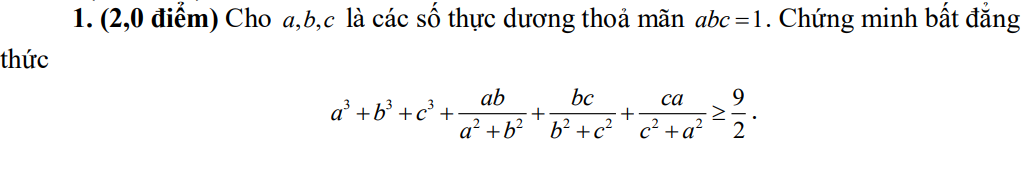Help me!!! Cần gấp ạ. Cảm ơn trc nha!!!