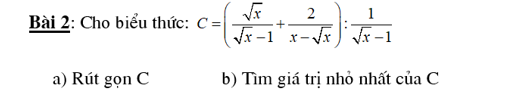Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot CB\)
=>\(BH\left(BH+3,6\right)=8^2=64\)
=>\(BH^2+3,6BH-64=0\)
=>(BH+10)(BH-6,4)=0
=>BH-6,4=0
=>BH=6,4(cm)
BC=BH+CH=6,4+3,6=10(cm)
Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{10^2-8^2}=6\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Tam giác `ABC` vuông tại A đường cao `AH`
`=> AB^2 = BH . AC`
`=> 8^2 = BH . (BH + 3,6) `
`=> BH = 6,4 (cm)`
`=> BC = 6,4 + 3,6 = 10 (cm) `
`=> AC = sqrt{BC^2 - AB^2} = sqrt{10^2 - 8^2} = 6 (cm)`
`=> AH = (AB . AC)/(BC) = (8.6)/10 = 4,8 (cm)`
 help me
help me


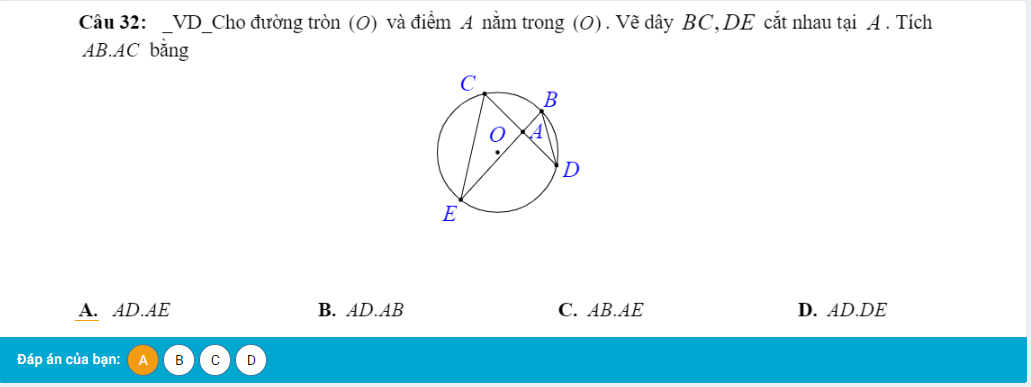
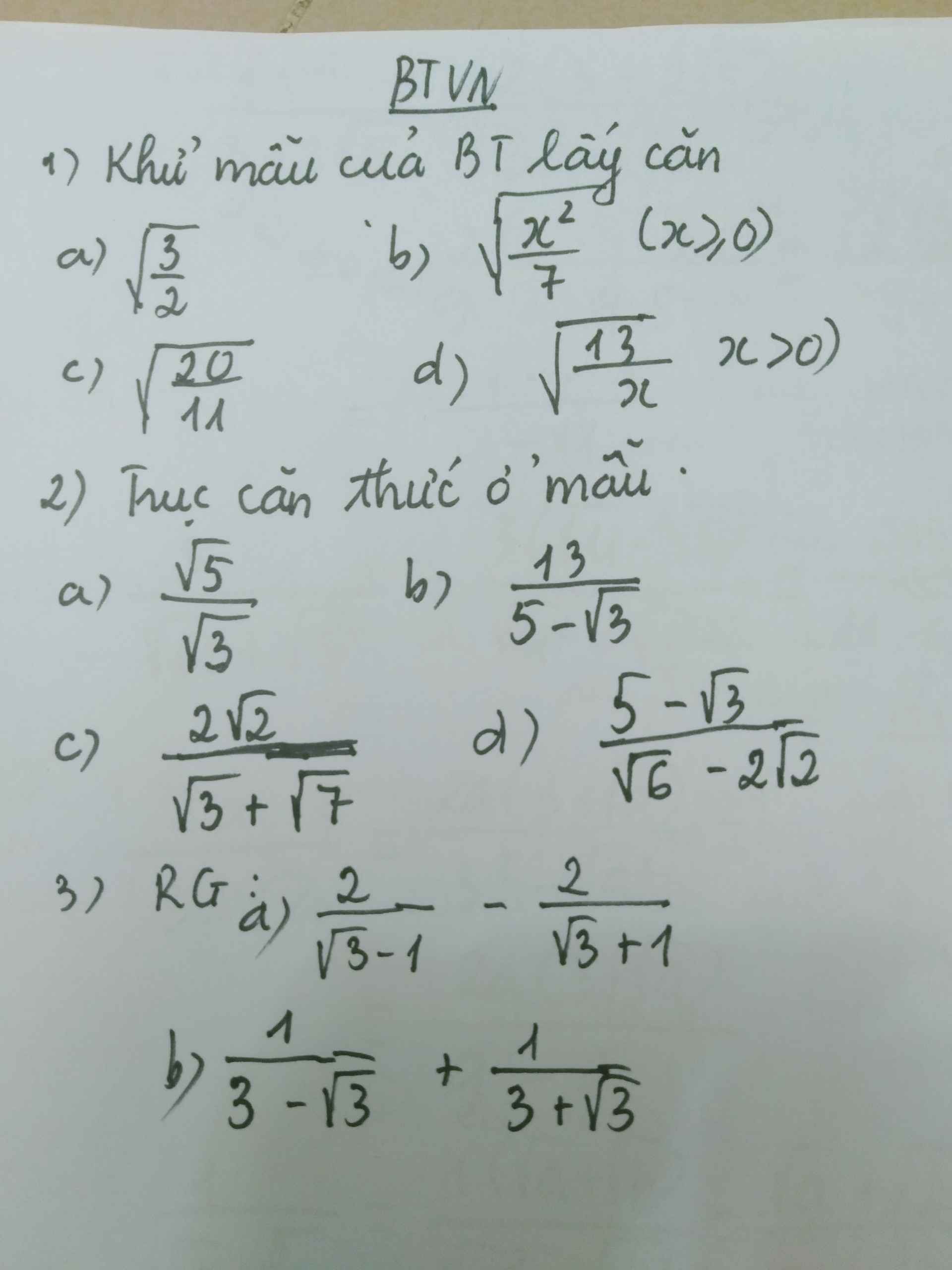
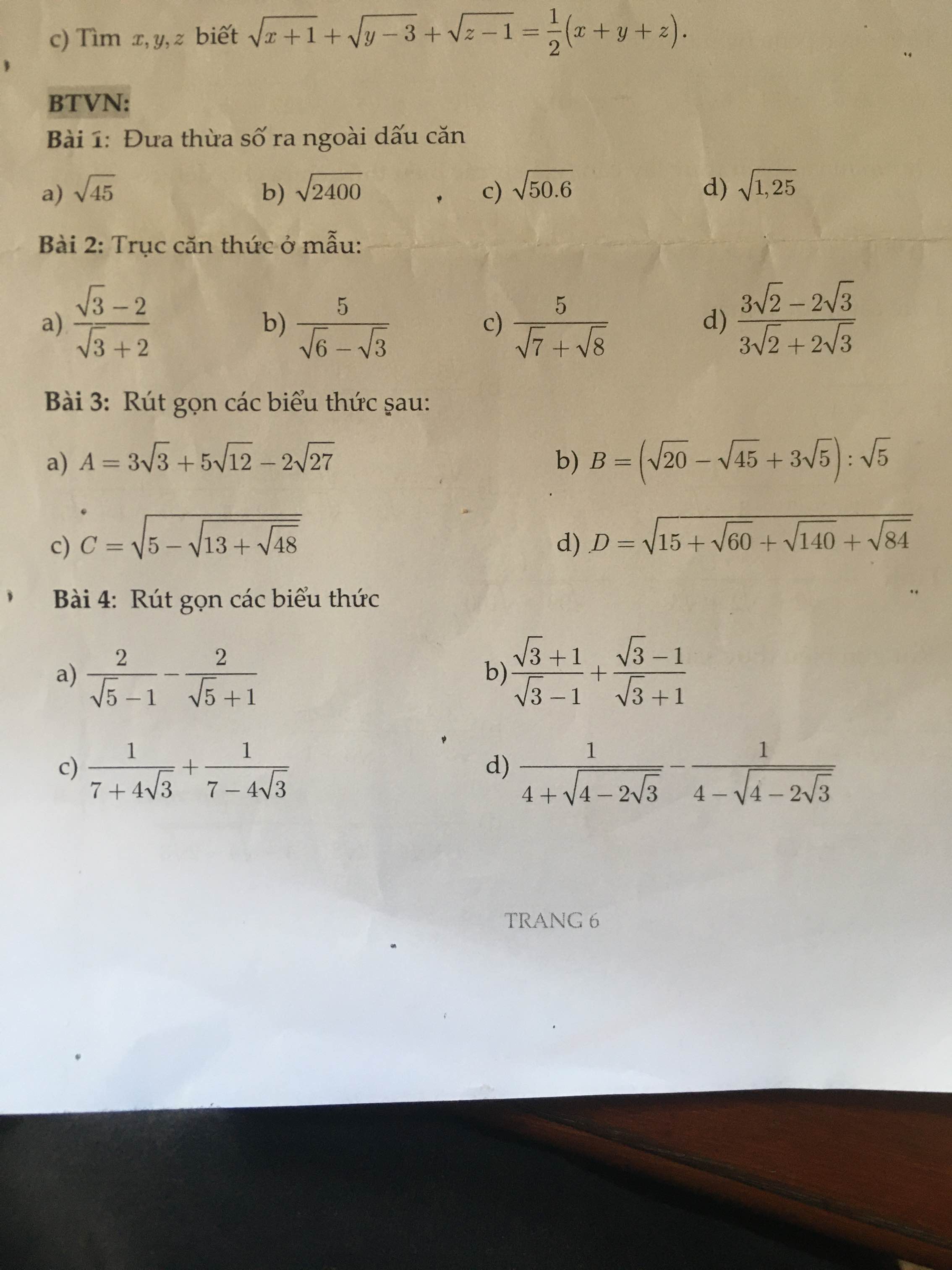
 HELP ME
HELP ME