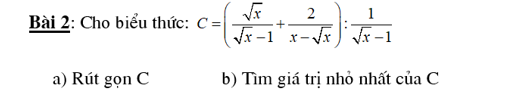`(x+1)/(x-1) - (x-1)/(x+1) = 16/(x^2-1)(ĐKXĐ: x≠1 , -1)`
\(\dfrac{\left(x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{16}{\left(x-1\right)\left(x+1\right)}\)
\(=\left(x+1\right)^2-\left(x-1\right)^2=16\)
`=> x^2 + 2x + 1 - (x^2 - 2x + 1) = 16`
`=>x^2 + 2x + 1 - x^2 + 2x - 1 =16`
`=> 4x = 16`
`=>x =4`
`b) (1- {x-1}/{x+1})(x+2)={x+1}/{x-1}+{x-1}/{x+1}` (ĐKXĐ:`x ne 1;-1`)
`<=> {x+1-x+1}/{x+1}(x+2)={(x+1)^{2}+(x-1)^2}/{(x-1)(x+1)}`
`<=> {2}/{x+1}(x+2)={x^{2}+2x+1+x^{2}-2x+1}/{(x-1)(x+1)}`
`<=> {2}/{x+1}(x+2)={2x^{2}+2}/{(x-1)(x+1)}`
`<=> {1}/{x+1}(x+2)={x^{2}+1}/{(x-1)(x+1)}`
`<=> (x-1)(x+2)=x^{2}+1`
`<=> x^{2}+x-2=x^{2}+1`
`<=> x=3` (thỏa mãn)

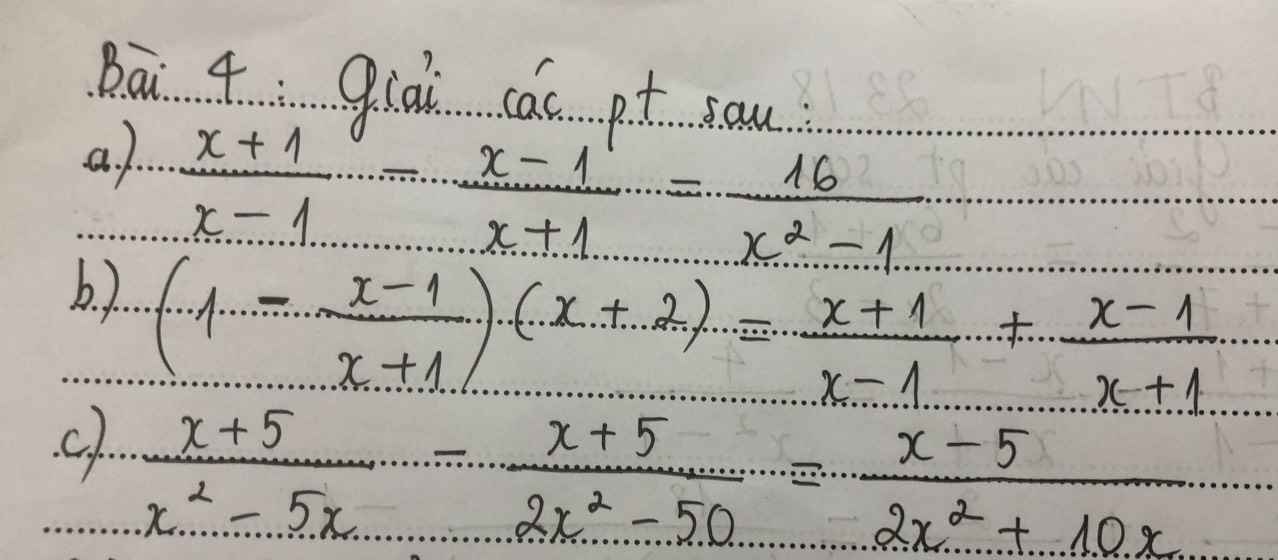



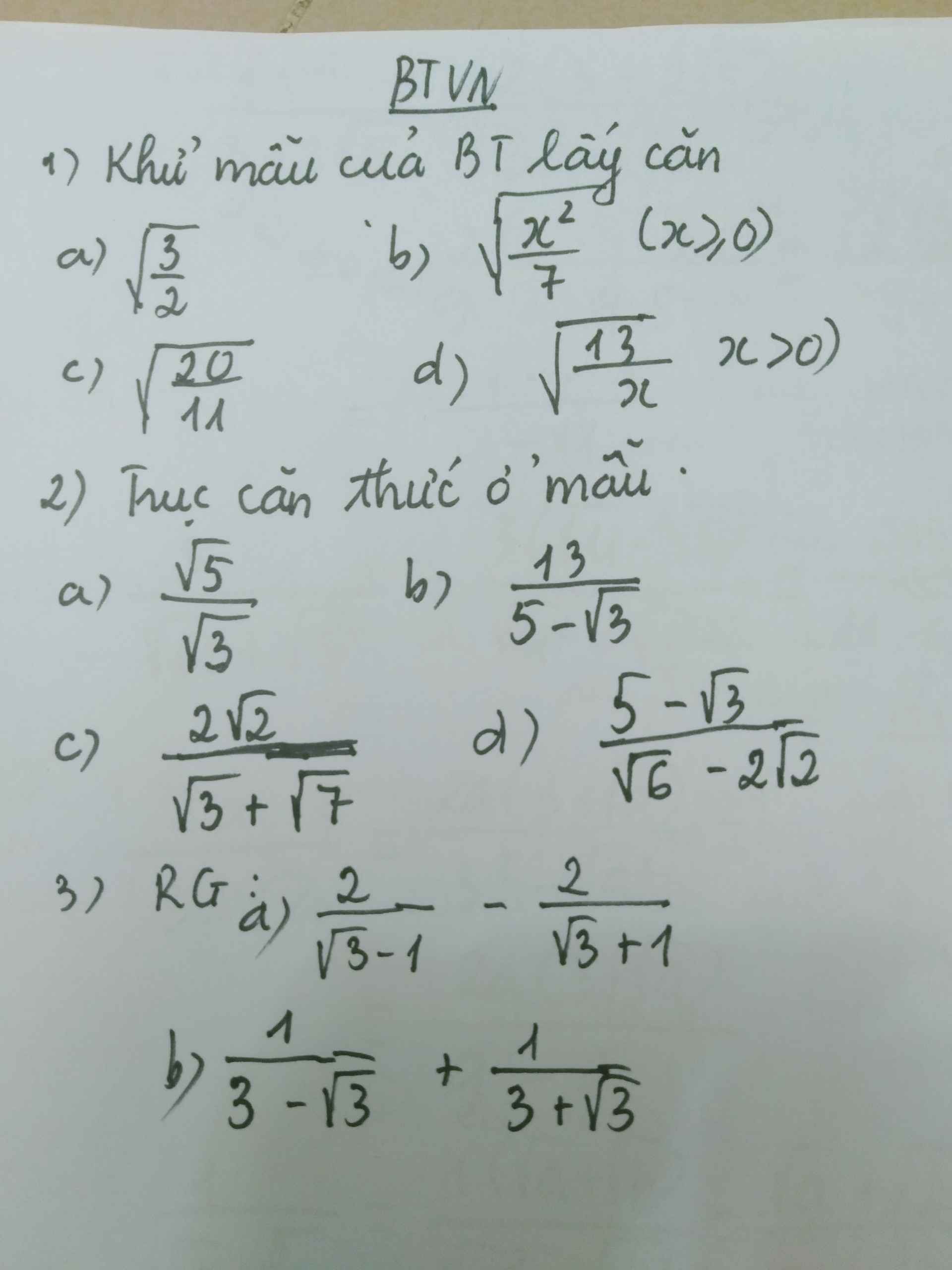
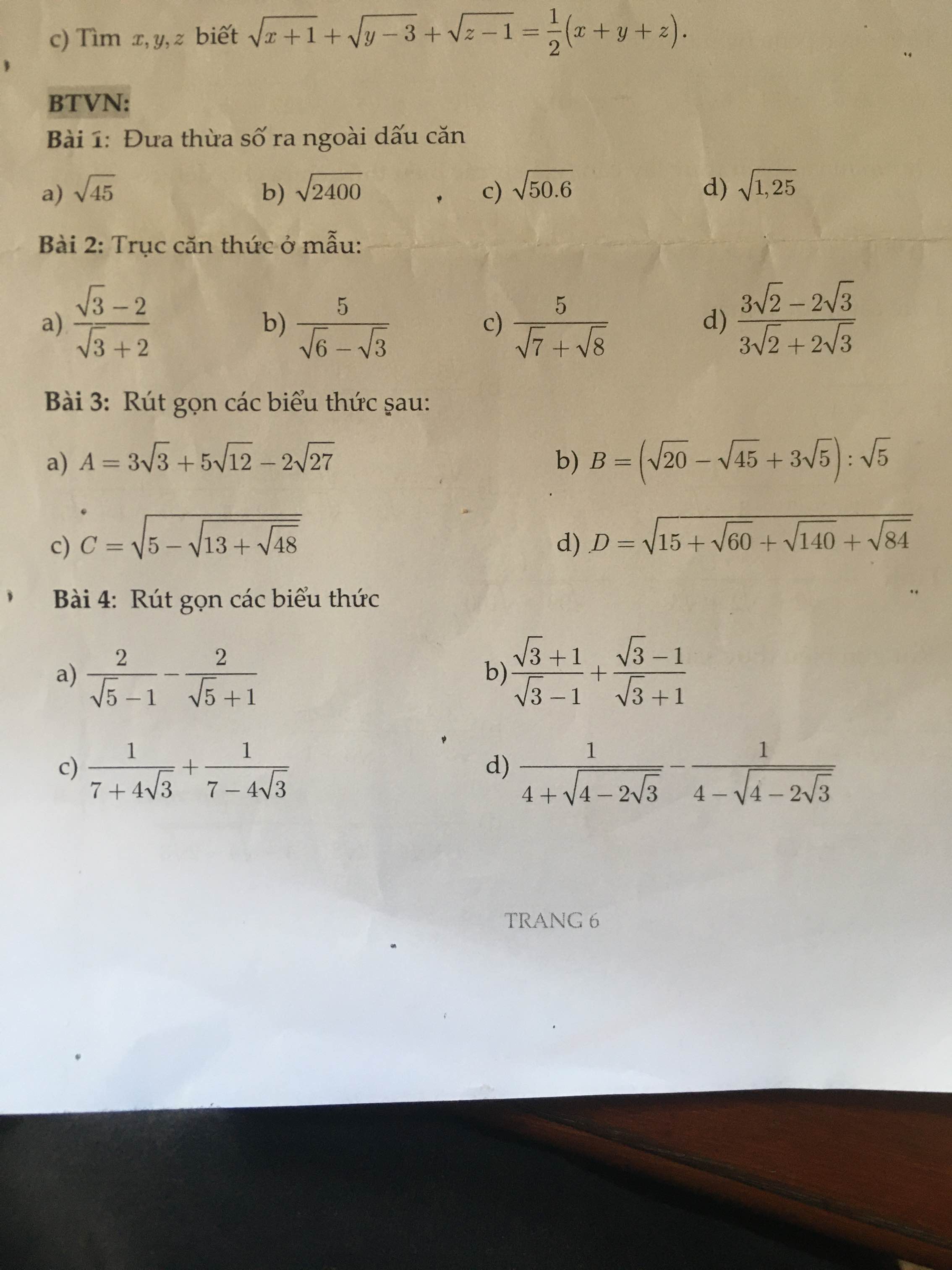
 HELP ME
HELP ME