Bài 5:
a: 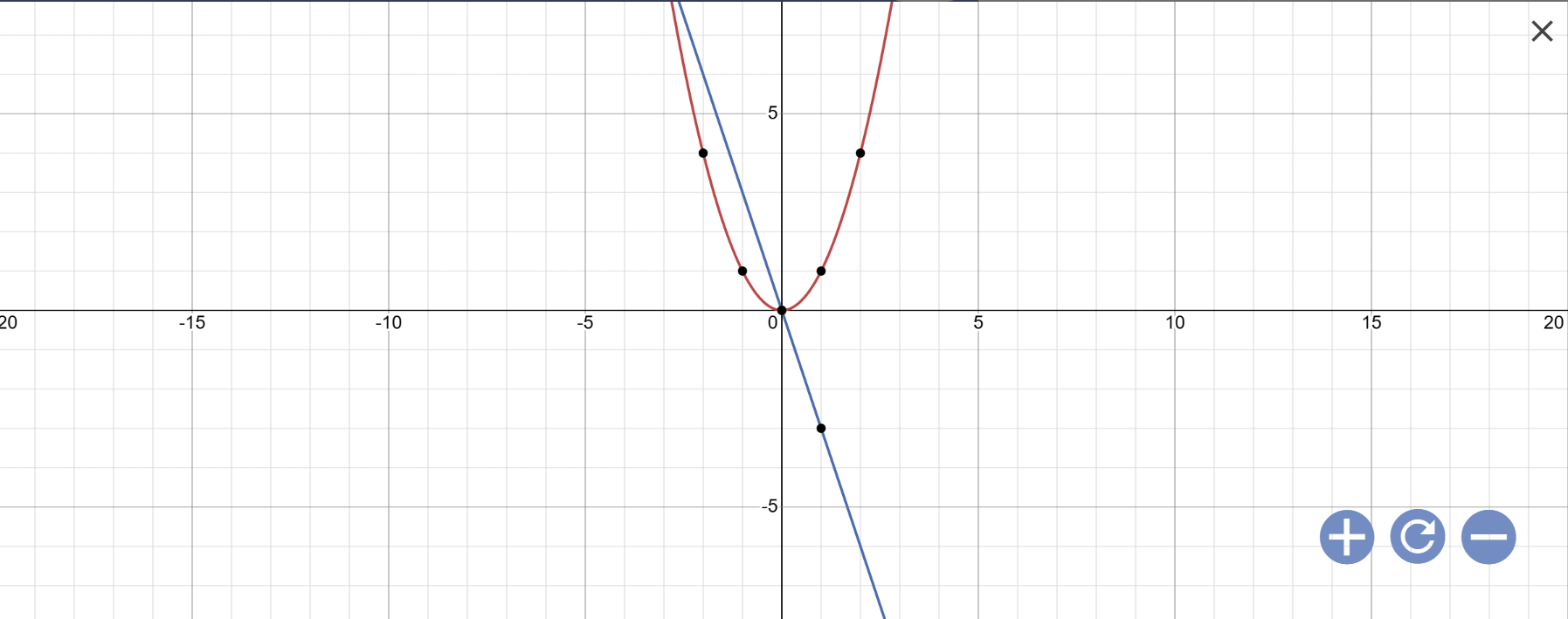
b: Phương trình hoành độ giao điểm là:
\(x^2=-3x\)
=>\(x^2+3x=0\)
=>x(x+3)=0
=>\(\left[{}\begin{matrix}x=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
Khi x=0 thì \(y=-3x-3\cdot0=0\)
Khi x=-3 thì \(y=\left(-3\right)^2=9\)
Vậy: Hai đồ thị hàm số \(y=x^2;y=-3x\) cắt nhau tại A(0;0); B(-3;9)
Bài 6:
a: Thay x=-2 và y=8 vào hàm số y=ax2, ta được:
\(a\cdot\left(-2\right)^2=8\)
=>4a=8
=>a=2
b: Khi a=2 thì \(y=2x^2\)
Vẽ đồ thị:
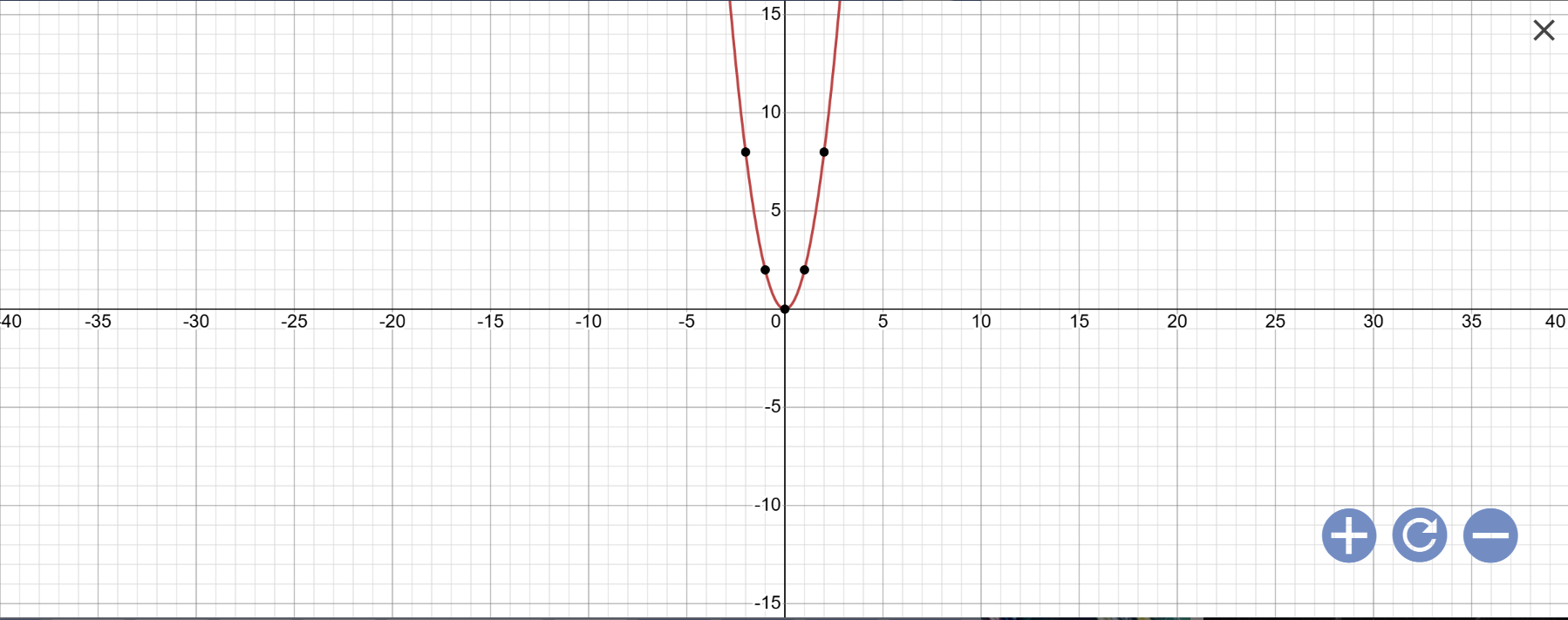
Khi x=3 thì \(y=2\cdot3^2=2\cdot9=18\ne-18\)
=>N(3;-18) không thuộc đồ thị hàm số \(y=2x^2\)
c: Thay y=x vào \(y=2x^2\), ta được:
\(2x^2=x\)
=>x(2x-1)=0
=>\(\left[{}\begin{matrix}x=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
Khi x=0 thì \(y=2x^2=2\cdot0^2=0\)
Khi x=1/2 thì \(y=2\cdot\left(\dfrac{1}{2}\right)^2=2\cdot\dfrac{1}{4}=\dfrac{1}{2}\)
Vậy: Tọa độ các điểm trên đồ thị hàm số \(y=2x^2\) mà cách đều hai trục tọa độ là O(0;0); C(1/2;1/2)



