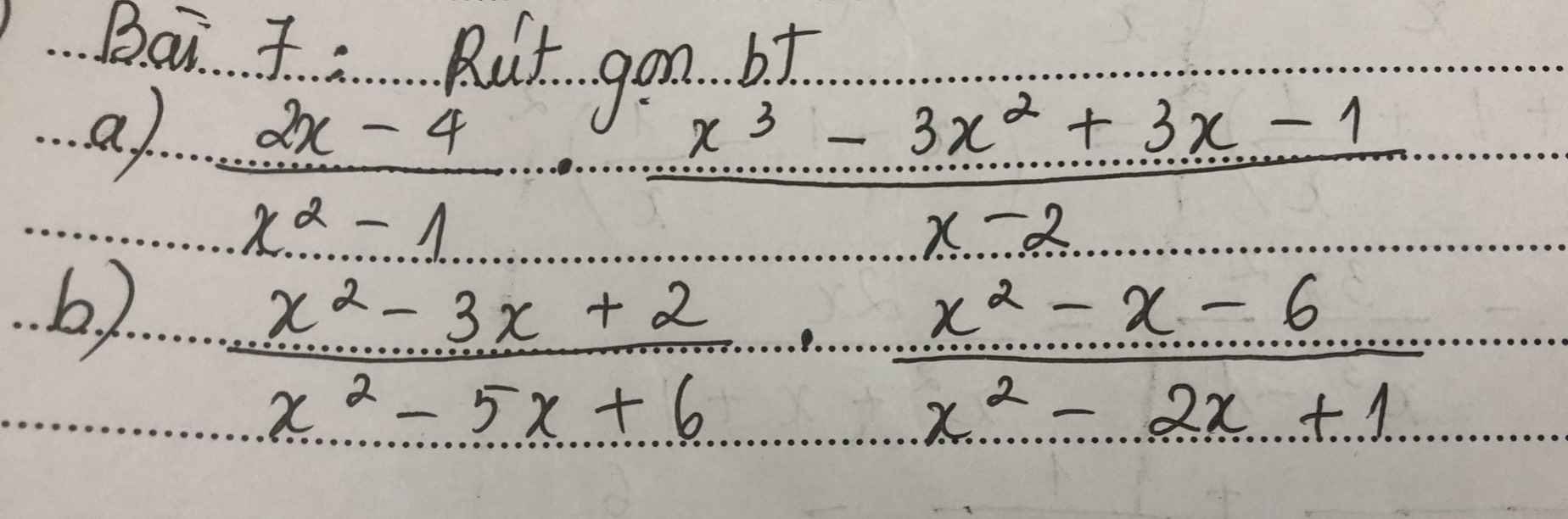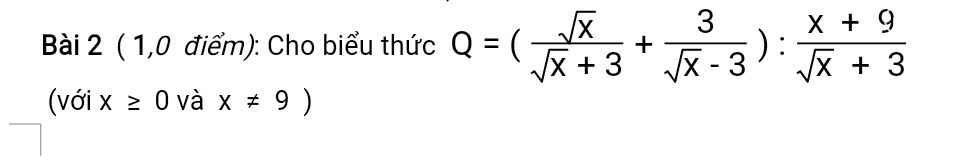a:
ĐKXĐ: \(x\notin\left\{1;-1;2\right\}\)
\(\dfrac{2x-4}{x^2-1}\cdot\dfrac{x^3-3x^2+3x-1}{x-2}\)
\(=\dfrac{2\left(x-2\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)^3}{x-2}\)
\(=\dfrac{2\left(x-1\right)^2}{x+1}\)
b:
ĐKXĐ: \(x\notin\left\{2;3;1\right\}\)
\(\dfrac{x^2-3x+2}{x^2-5x+6}\cdot\dfrac{x^2-x-6}{x^2-2x+1}\)
\(=\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-2\right)\left(x-3\right)}\cdot\dfrac{\left(x-3\right)\left(x+2\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x-1}{x-3}\cdot\dfrac{\left(x-3\right)\left(x+2\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x-1}{\left(x-1\right)^2}\cdot\left(x+2\right)=\dfrac{x+2}{x-1}\)
a) \(\dfrac{2x-4}{x^2-1}.\dfrac{x^3-3x^2+3x-1}{x-2}\) (ĐKXĐ:\(x\ne1;-1;2\))
\(=\dfrac{2\left(x-2\right)\left(x^3-3.x^2.1+3.x.1^2-1^3\right)}{\left(x^2-1^2\right)\left(x-2\right)}\)
\(=\dfrac{2\left(x-1\right)^3}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{2\left(x-1\right)^2}{x+1}\)
b) \(\dfrac{x^2-3x+2}{x^2-5x+6}.\dfrac{x^2-x-6}{x^2-2x+1}\) (ĐKXĐ:\(x\ne2;3;1\))
\(=\dfrac{\left(x^2-x-2x+2\right)\left(x^2-3x+2x-6\right)}{\left(x^2-2x-3x+6\right)\left(x^2-x-x+1\right)}\)
\(=\dfrac{\left[x\left(x-1\right)-2\left(x-1\right)\right].\left[x\left(x-3\right)+2\left(x-3\right)\right]}{\left[x\left(x-2\right)-3\left(x-2\right)\right]\left[x\left(x-1\right)-1\left(x-1\right)\right]}\)
\(=\dfrac{\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x-3\right)}{\left(x-3\right)\left(x-2\right)\left(x-1\right)\left(x-1\right)}\)
\(=\dfrac{x+2}{x-1}\)