a: \(x^4-5x^2+4=0\)
=>\(\left(x^2-1\right)\left(x^2-4\right)=0\)
=>(x-1)(x+1)(x-2)(x+2)=0
=>\(\left[{}\begin{matrix}x-1=0\\x+1=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=2\\x=-2\end{matrix}\right.\)
b: \(5x^4-22x^2+17=0\)
=>\(5x^4-5x^2-17x^2+17=0\)
=>\(\left(x^2-1\right)\left(5x^2-17\right)=0\)
=>\(\left[{}\begin{matrix}x^2=1\\x^2=\dfrac{17}{15}\end{matrix}\right.\Leftrightarrow x\in\left\{1;-1;\sqrt{\dfrac{17}{15}};-\sqrt{\dfrac{17}{15}}\right\}\)
c: \(0,3x^4+1,8x^2+1,5=0\)
=>\(x^4+6x^2+5=0\)
mà \(x^4+6x^2+5=x^2\left(x^2+6\right)+5>=0+5=5>0\forall x\)
nên phương trình vô nghiệm
d:
ĐKXĐ: x<>0
\(\left(\dfrac{x^2-1}{x}\right)^2-4\cdot\dfrac{x^2-1}{x}=12\)
=>\(\left(\dfrac{x^2-1}{x}\right)^2-4\cdot\dfrac{x^2-1}{x}-12=0\)
=>\(\left(\dfrac{x^2-1}{x}-6\right)\left(\dfrac{x^2-1}{x}+2\right)=0\)
=>\(\dfrac{x^2-6x-1}{x}\cdot\dfrac{x^2+2x-1}{x}=0\)
=>\(\left(x^2-6x-1\right)\left(x^2+2x-1\right)=0\)
=>\(\left[{}\begin{matrix}x^2-6x-1=0\\x^2+2x-1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x^2-6x+9=10\\x^2+2x+1=2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(x-3\right)^2=10\\\left(x+1\right)^2=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-3\in\left\{\sqrt{10};-\sqrt{10}\right\}\\x+1\in\left\{\sqrt{2};-\sqrt{2}\right\}\end{matrix}\right.\)
=>\(x\in\left\{\sqrt{10}+3;-\sqrt{10}+3;\sqrt{2}-1;-\sqrt{2}-1\right\}\)
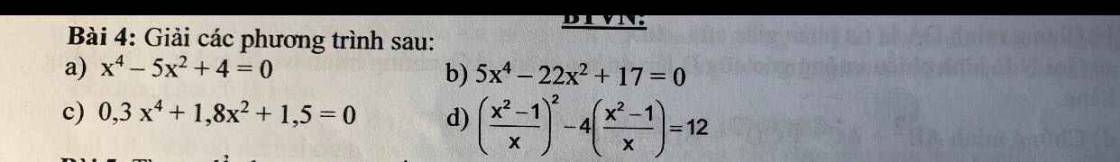 hãy cứu tui
hãy cứu tui