Chọn A
Ta có;
Hàm số y = sinx đồng biến trên mỗi khoảng 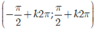
Chọn A
Ta có;
Hàm số y = sinx đồng biến trên mỗi khoảng 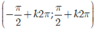
Trong các hàm số sau hàm số nào là đồng biến trên khoảng (-π;0)
A. y = tanx
B. y = cotx
C. y = sinx
D. y = cosx
Cho các mệnh đề sau
(I) Hàm số f(x) = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f(x) = 3sinx + 4cosx có giá trị lớn nhất là 5.
(III) Hàm số f(x) = tanx tuần hoàn với chu kì 2 π .
(IV) Hàm số f(x) = cosx đồng biến trên khoảng (0; π )
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4
B. 2
C. 3
D. 1
Có bao nhiêu số nguyên âm m để hàm số y = 1 3 c o s 3 x - 4 c o t x - ( m + 1 ) cos x đồng biến trên khoảng ( 0 ; π ) ?
A. 5
B. 2
C. vô số
D. 3
Sử dụng máy tính bỏ túi, hãy tính sinx, cosx với x là các số sau:
π/6; π/4; 1,5; 2; 3,1; 4,25; 5.
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
A. 1 nghiệm.
B. 2 nghiệm.
C. 3 nghiệm.
D. 4 nghiệm.
Cho hàm số y = cos2x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)
A. 1 nghiệm.
B. 2 nghiệm.
C. 3 nghiệm.
D. 4 nghiệm.
Tìm giá trị lớn nhất của hàm số sau y = sinx - 1 sinx trong khoảng 0 < x < π
A: -1
B: 0
C: 1
D: 2
sin ( x + π 4 ) + sin ( x − π 4 ) = 0 thuộc khoảng (0;4π)
Chu kì của hàm số y = 2 sin ( 2 x + π / 3 ) - 3 cos ( 2 x - π / 4 ) là:
A. 2π
B. π
C. π/2
D. 4 π
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).