Đáp án C
TH1: a = b = 0 thì y = cx + d.Để hàm số đồng biến trên − ∞ ; + ∞ thì c > 0.
TH2: a ≠ 0 , em có: y ' = 3 ax 2 + 2 bx + c . Để hàm số đồng biến trên − ∞ ; + ∞⇔ y ' ≥ 0 ⇔ a > 0 Δ y ' ≤ 0 ⇔ a > 0 b 2 − 3 a c ≤ 0
Đáp án C
TH1: a = b = 0 thì y = cx + d.Để hàm số đồng biến trên − ∞ ; + ∞ thì c > 0.
TH2: a ≠ 0 , em có: y ' = 3 ax 2 + 2 bx + c . Để hàm số đồng biến trên − ∞ ; + ∞⇔ y ' ≥ 0 ⇔ a > 0 Δ y ' ≤ 0 ⇔ a > 0 b 2 − 3 a c ≤ 0
Cho 3 số a, b, c > 0, a ≠ 1 , b ≠ 1 , c ≠ 1 . Đồ thị các hàm số y = a x , y = b x , c = c x . được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng ?
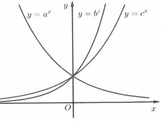
A. b < c < a
B. a < c < b
C. a < b < c
D. c < a < b
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Hàm số y = a x 3 + b x 2 + c x + d , a ≠ 0 luôn đồng biến trên ℝ khi và chỉ khi
A. a > 0 b 2 − a c < 0
B. a > 0 b 2 − 3 a c < 0
C. a > 0 b 2 − 3 a c > 0
D. a > 0 b 2 − 3 a c ≤ 0
Cho hàm số y = a x 3 + bx 2 + c x + d có bảng biến thiên:
Cho các mệnh đề:
(1) Hệ số b < 0
(2) Hàm số có y CD = 2 ; y CT = - 2
(3) y''(0) < 0
(4) Hệ số c = 0, d = 1
Có bao nhiêu mệnh đề đúng:
A. 1
B. 2
C. 3
D. 4
Cho 3 số a , b , c > 0 , a ≠ 1 , b ≠ 1 , c ≠ 1. Đồ thị các hàm số y = a x , y = a x , y = c x được cho trong hình vẽ dưới.

Mệnh đề nào sau đây đúng?
A. b < c < a
B. a < c < b
C. a < b < c
D. c < a < b
Cho hàm số
y
=
ax
+
b
x
+
c
có bảng biến thiên dưới đây:\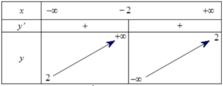
Cho các mệnh đề:
(1) Hàm số đồng biến trên toàn tập xác định.
(2) Hệ số a = 2, c = 2
(3) Nếu y ' = 3 x + 2 2 thì b = 1
(4) Đồ thị hàm số nhận giao của 2 đường tiệm cận I(-2;2) là tâm đối xứng.
Có bao nhiêu mệnh đề sai?
A. 4
B. 3
C. 1
D. 0
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Cho a,b,c∈R sao cho hàm số y=x 3 + ax 2 + bx + c đạt cực trị tại x = 2 đồng thời có y(0)=1 và y(2)=-3. Hỏi trong không gian Oxyz, điểm M(a;b;c) nằm trong mặt cầu nào sau đây?
A. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 16 .
B. ( x - 2 ) 2 + ( y - 3 ) 2 + ( z + 5 ) 2 = 64 .
C. x 2 + y 2 + ( z + 5 ) 2 = 36 .
D. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 .