Ta có y’=12x2+2mx-3.
Do ∆ ' = m 2 + 36 > 0 , ∀ m ∈ ℝ nên hàm số luôn có hai điểm cực trị x1; x2.
Theo Viet, ta có x 1 + x 2 = - m 6 x 1 x 2 = - 1 4
Mà x1+4x2=0 suy ra
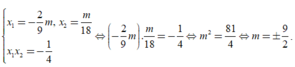
Chọn A.
Ta có y’=12x2+2mx-3.
Do ∆ ' = m 2 + 36 > 0 , ∀ m ∈ ℝ nên hàm số luôn có hai điểm cực trị x1; x2.
Theo Viet, ta có x 1 + x 2 = - m 6 x 1 x 2 = - 1 4
Mà x1+4x2=0 suy ra
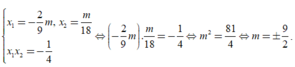
Chọn A.
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 3 x 3 - m x 2 - 2 ( 3 m 2 - 1 ) x + 2 3 có hai điểm cực trị có hoành độ x 1 , x 2 sao cho x 1 x 2 + 2 ( x 1 + x 2 ) = 1
A. m = 0
B. m = - 2 3
C. m = 2 3
D. m = - 1 2
Gọi x 1 , x 2 là hai điểm cực trị của hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m . Tìm tất cả các giá trị của tham số thực m để : x 1 2 + x 2 2 - x 1 x 2 = 7
A. m = ± 2 .
B. m = ± 2 .
C. m = 0 .
D. m = ± 1 .
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Cho hàm số y = x 3 - 3 x 2 + m x - 1 với m là tham số thực. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x 1 , x 2 thỏa x 1 2 + x 2 2 = 6 .
A. 3.
B. -1.
C. 1.
D. -3.
Tìm tất các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m + 3 ) x 2 + 4 ( m + 3 ) x + m 3 - m đạt cực trị tại x 1 , x 2 thỏa mãn -2< x 1 < x 2
A. m< -2.
B. m< 1.
C. m< -3
D. m>3
Tìm tất các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m + 3 ) x 2 + 4 ( m + 3 ) x + m 3 - m đạt cực trị tại x 1 , x 2 thỏa mãn - 1 < x 1 < x 2
A. - 7 2 < m < - 2 .
B. - 3 < m < 1 .
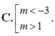
D. - 7 2 < m < - 3 .
Tìm tất cả các giá trị thực của m để hàm số y = x 3 3 - ( m - 2 ) x 2 + ( 4 m - 8 ) x + m + 1 đạt cực trị tại các điểm x1, x2 sao cho x 1 < - 2 < x 2 .
A. m ⩾ 1 .
B. m > 1 2 .
C. m ⩽ 2 .
D. m < 3 2 .
Tìm các giá trị của tham số m để hàm số: y = 1 3 m x 3 - ( m - 1 ) x 2 + 3 ( m - 2 ) x + 1 6 đạt cực trị tại x 1 , x 2 thỏa mãn x 1 + 2 x 2 = 1
A. 1 - 6 2 < m < 1 + 6 2 .
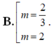
C. m ∈ 1 - 6 2 ; 1 + 6 2 \ 0 .
D. m = 2 .