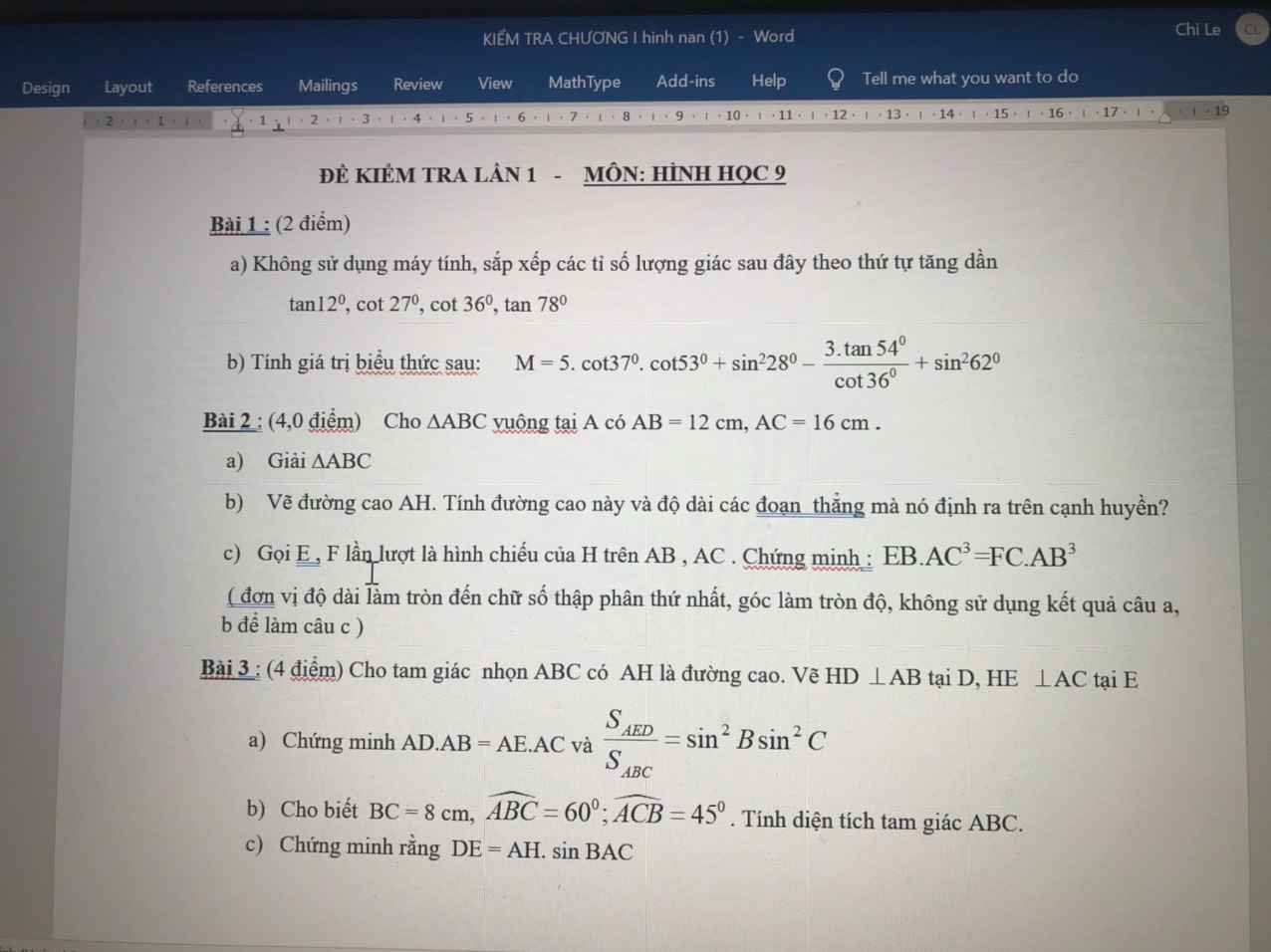
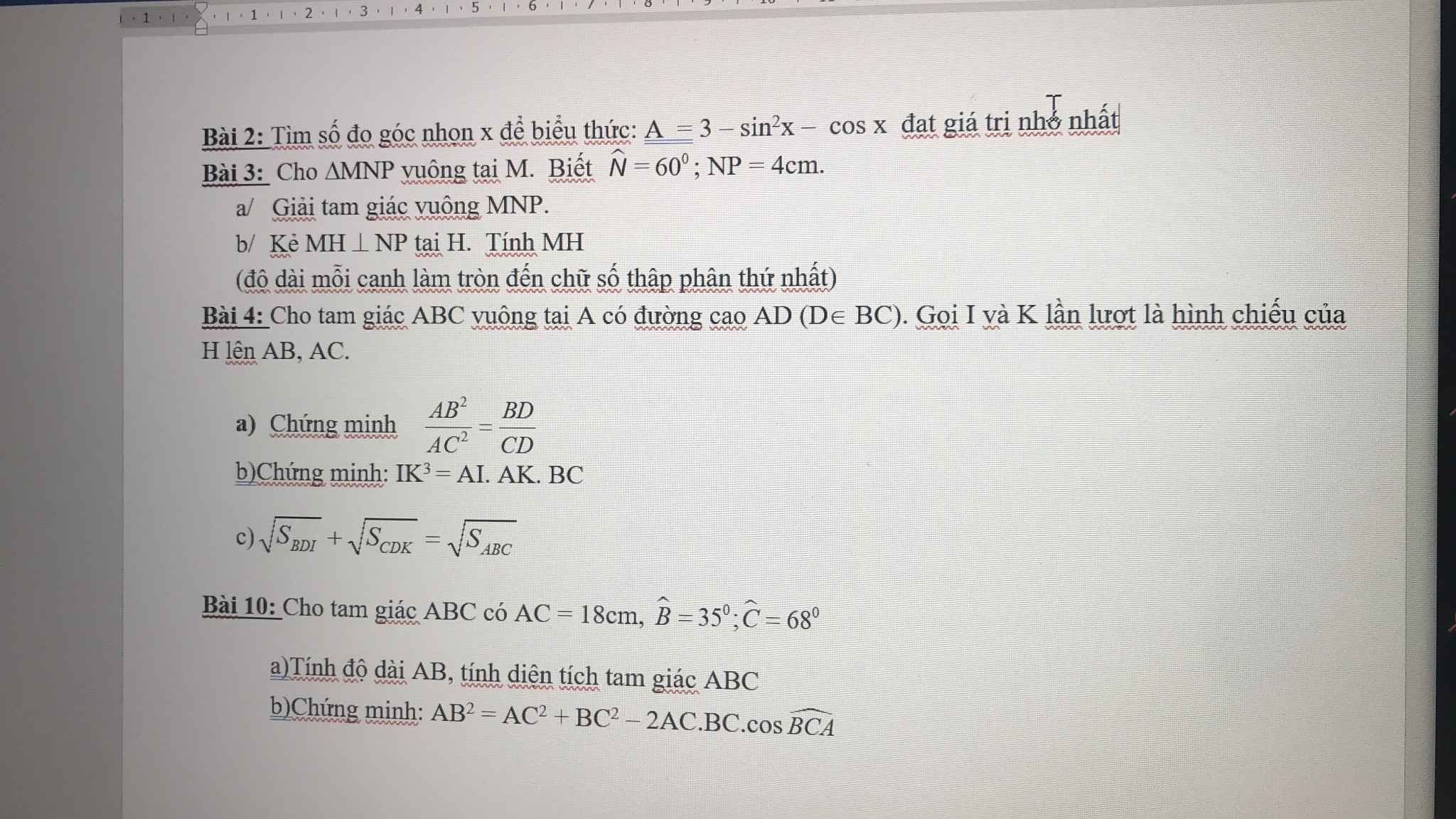Xét \(\Delta AMO\) vuông tại M
=> \(AO^2=AM^2+MO^2\)
\(\Leftrightarrow AM^2=AO^2-MO^2\)
Chứng minh tương tự :
\(BP^2=BO^2-OP^2\)
\(CN^2=CO^2-NO^2\)
\(BO^2=BM^2+MO^2\)
\(CO^2=PO^2+PC^2\)
\(AO^2=AN^2+NO^2\)
Có ;
\(AM^2+BO^2+BP^2+CO^2+CN^2+AO^2=AO^2-MO^2+BO^2-OP^2+CO^2-NO^2+BM^2+MO^2+PO^2+PC^2+AN^2+NO^2\)
=> \(AM^2+BO^2+BP^2+CO^2+CN^2+AO^2=AO^2+BO^2+CO^2+BM^2-PC^2+AN^2\)
=> \(AM^2+BP^2+CN^2=BM^2-PC^2+AN^2\left(đpcm\right)\)