Lời giải:
Để $Q$ có nghĩa thì $x>0$ và $x\neq 1$
\(Q=\left[\frac{1}{\sqrt{x}(\sqrt{x}-1)}+\frac{\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)}\right]:\frac{\sqrt{x}+1}{(\sqrt{x}-1)^2}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)}.\frac{(\sqrt{x}-1)^2}{\sqrt{x}+1}=\frac{\sqrt{x}-1}{\sqrt{x}}\)
\(Q=1-\frac{1}{\sqrt{x}}<1\) do $\frac{1}{\sqrt{x}}>0$
Đúng 1
Bình luận (0)




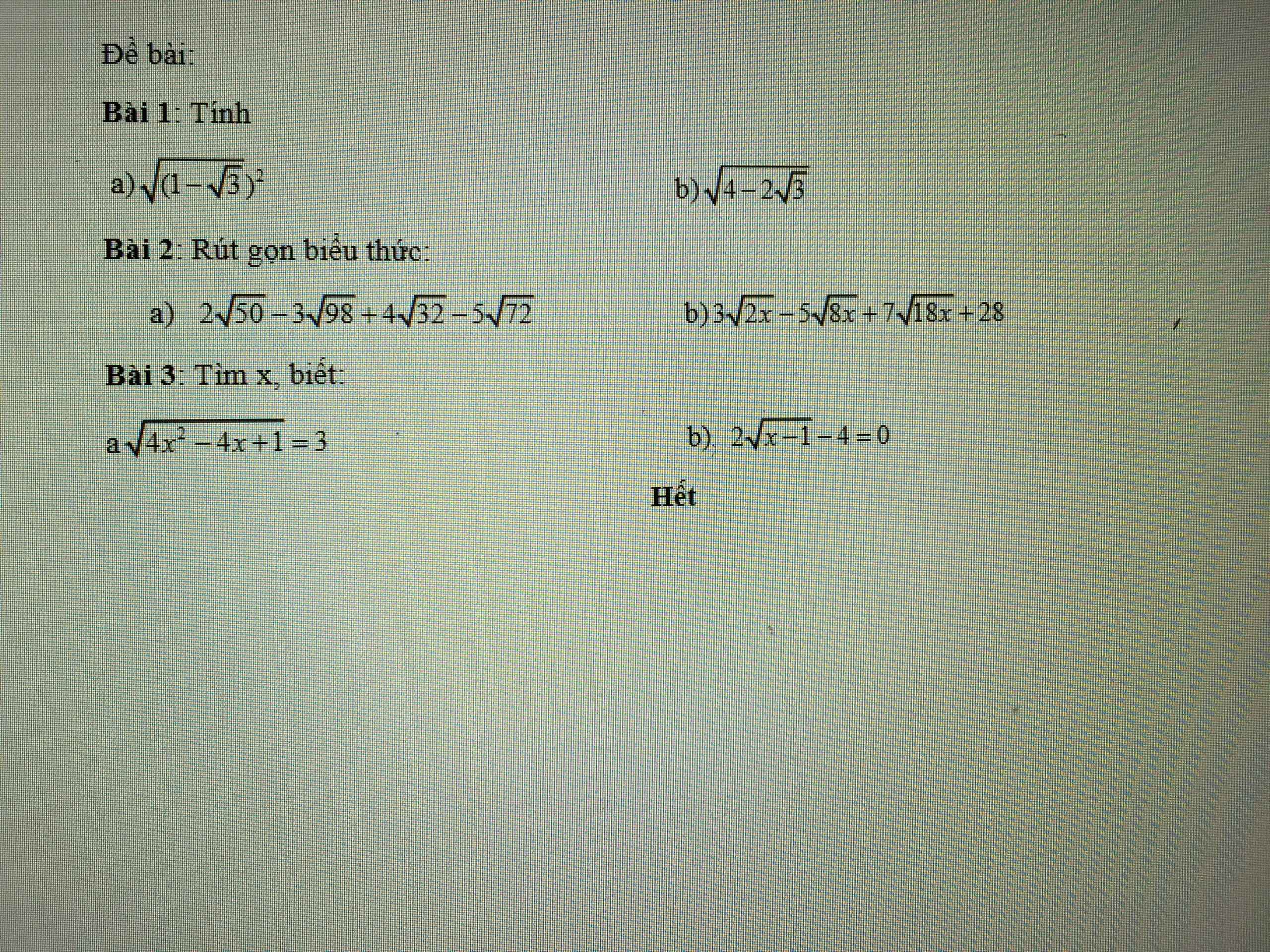 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!