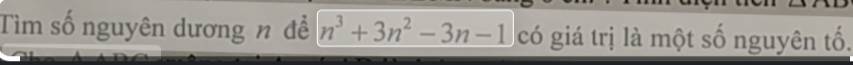\(n^3+3n^2-3n-1=\left(n-1\right)\left(n^2+n+1\right)+3n\left(n-1\right)\)
\(=\left(n-1\right)\left(n^2+4n+1\right)\)
Để \(n^3+3n^2-3n-1\) có giá trị là số nguyên tố thì:
\(\left[{}\begin{matrix}n-1=1\\n^2+4n+1=1\end{matrix}\right.\Rightarrow n=2\) (vì n là số nguyên dương).
Với \(n=2\) thì \(n^3+3n^2-3n-1=13\) là số nguyên tố (thỏa mãn).
Vậy \(n=2\)
Đúng 0
Bình luận (0)