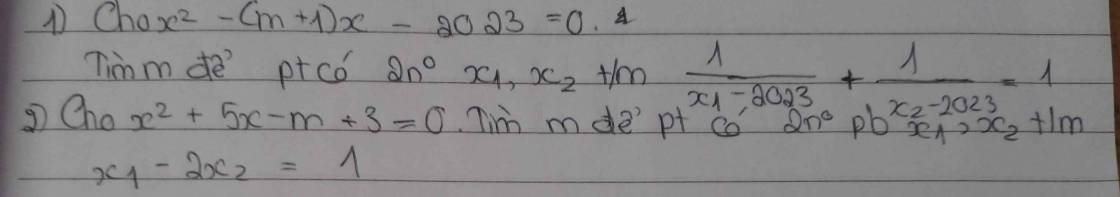Question

giúp tớ nhé,cảm ơn mn trc ><

Answer 1

1: \(x^2-\left(m+1\right)x-2023=0\)

a=1; b=-(m+1); c=-2023

Vì \(a\cdot c=-2023< 0\)

nên phương trình luôn có hai nghiệm phân biệt

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(m+1\right)\right]}{1}=m+1\\x_2\cdot x_1=\dfrac{c}{a}=-\dfrac{2023}{1}=-2023\end{matrix}\right.\)

\(\dfrac{1}{x_1-2023}+\dfrac{1}{x_2-2023}=1\)

=>\(\dfrac{x_2-2023+x_1-2023}{\left(x_1-2023\right)\left(x_2-2023\right)}=1\)

=>\(x_2+x_1-4046=\left(x_1-2023\right)\left(x_2-2023\right)\)

=>\(m+1-4046=x_1x_2-2023\left(x_1+x_2\right)+2023^2\)

=>\(m-4045=-2023-2023\left(m+1\right)+2023^2\)

=>\(m-4045=-2023-2023m-2023+2023^2\)

=>\(2024m=4092528\)

=>\(m=\dfrac{4092528}{2024}=2022\)