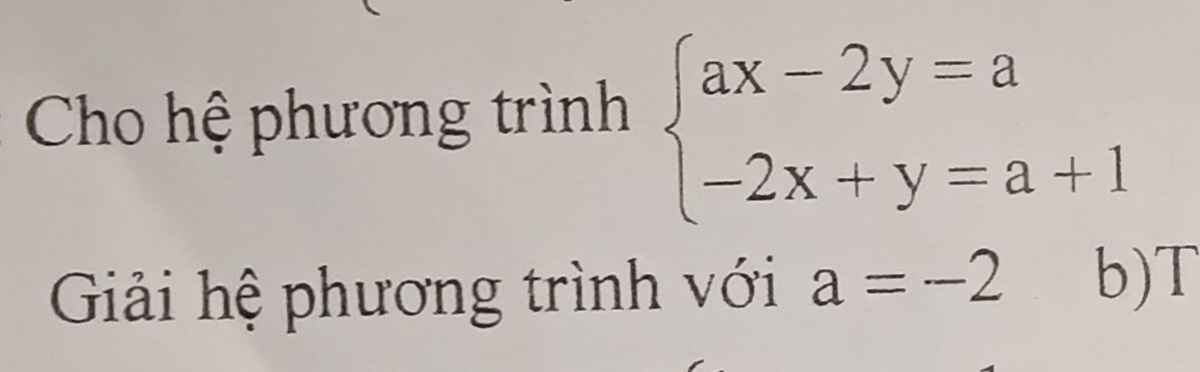2a.
Từ pt ta có:
\(\left\{{}\begin{matrix}x.1=2\\y.2=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
\(2Ag+Cl_2=2AgCl\)
b.
Do (-2;1) là 1 cặp nghiệm của hệ, thay vào hệ ban đầu ta được:
\(\left\{{}\begin{matrix}2m.\left(-2\right)+1=m\\-2-m.1=-1-6m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4m+1=m\\-2-m=-1-6m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5m=1\\5m=1\end{matrix}\right.\)
\(\Leftrightarrow m=\dfrac{1}{5}\)
c.
Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y (x;y là các chữ số từ 0 tới 9, x khác 0)
Do đổi chỗ 2 chữ số ta được số mới lớn hơn số đã cho là 63 đơn vị nên:
\(\overline{yx}-\overline{xy}=63\Leftrightarrow\left(10y+x\right)-\left(10x+y\right)=63\)
\(\Leftrightarrow-x+y=7\) (1)
Do tổng của số mới và số cũ là 99 nên:
\(\overline{xy}+\overline{yx}=99\Leftrightarrow\left(10x+y\right)+\left(10y+x\right)=99\)
\(\Leftrightarrow x+y=9\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}-x+y=7\\x+y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=8\end{matrix}\right.\)
Vậy số đó là 18
Em cần bài nào trong mấy bài này nhỉ?
3.
a.
\(A=cos40^0-sin50^0+tan20^0.cot20^0\)
\(=cos\left(90^0-50^0\right)-sin50^0+tan20^0.\left(\dfrac{1}{tan20^0}\right)\)
\(=sin50^0-sin50^0+1\)
\(=0+1=1\)
b.
\(B=\dfrac{sin10^0}{cos80^0}-\dfrac{cos20^0}{sin70^0}+\dfrac{tan15^0}{cot75^0}\)
\(=\dfrac{sin10^0}{cos\left(90^0-10^0\right)}-\dfrac{cos20^0}{sin\left(90^0-20^0\right)}+\dfrac{tan15^0}{cot\left(90^0-15^0\right)}\)
\(=\dfrac{sin10^0}{sin10^0}-\dfrac{cos20^0}{cos20^0}+\dfrac{tan15^0}{tan15^0}\)
\(=1-1+1=1\)
4.
a.
Ta có: \(\widehat{C}=\widehat{CBx}=25^0\) (so le trong)
Trong tam giác vuông ABC:
\(tan\widehat{C}=\dfrac{AB}{AC}\Rightarrow AB=AC.tan\widehat{C}=1221.tan25^0=569\left(m\right)\)
Độ cao đài quan sát: \(569+3=572\left(m\right)\)
b.
Ta có: \(CD=60.\dfrac{1}{60}=1\left(km\right)=1000\left(m\right)\)
\(\Rightarrow AD=AC-CD=221\left(m\right)\)
Trong tam giác vuông ACD:
\(tan\widehat{BDA}=\dfrac{AB}{AD}=\dfrac{569}{221}\Rightarrow\widehat{BDA}\approx68^046'\)
\(\Rightarrow\alpha=\widehat{BDA}=68^046'\) (so le trong)
c.
Trong tam giác vuông ABD:
\(BD=\sqrt{AB^2+AD^2}=\sqrt{569^2+221^2}=610\left(m\right)\)
5.
Với mọi số thực dương a;b ta có:
\(\left(a-b\right)^2\ge0\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2+2ab\ge4ab\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
Áp dụng:
\(\dfrac{1}{2x+y+z}=\dfrac{1}{\left(x+y\right)+\left(x+z\right)}\le\dfrac{1}{4}\left(\dfrac{1}{x+y}+\dfrac{1}{x+z}\right)\le\dfrac{1}{4}\left[\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{z}\right)\right]\)
\(\Rightarrow\dfrac{1}{2x+y+z}\le\dfrac{1}{8x}+\dfrac{1}{16y}+\dfrac{1}{16z}\)
Tương tự:
\(\dfrac{1}{x+2y+z}\le\dfrac{1}{16x}+\dfrac{1}{8y}+\dfrac{1}{16z}\)
\(\dfrac{1}{x+y+2z}\le\dfrac{1}{16x}+\dfrac{1}{16y}+\dfrac{1}{8z}\)
Cộng vế:
\(\dfrac{1}{2x+y+z}+\dfrac{1}{x+2y+z}+\dfrac{1}{x+y+2z}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=1\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=\dfrac{3}{4}\)