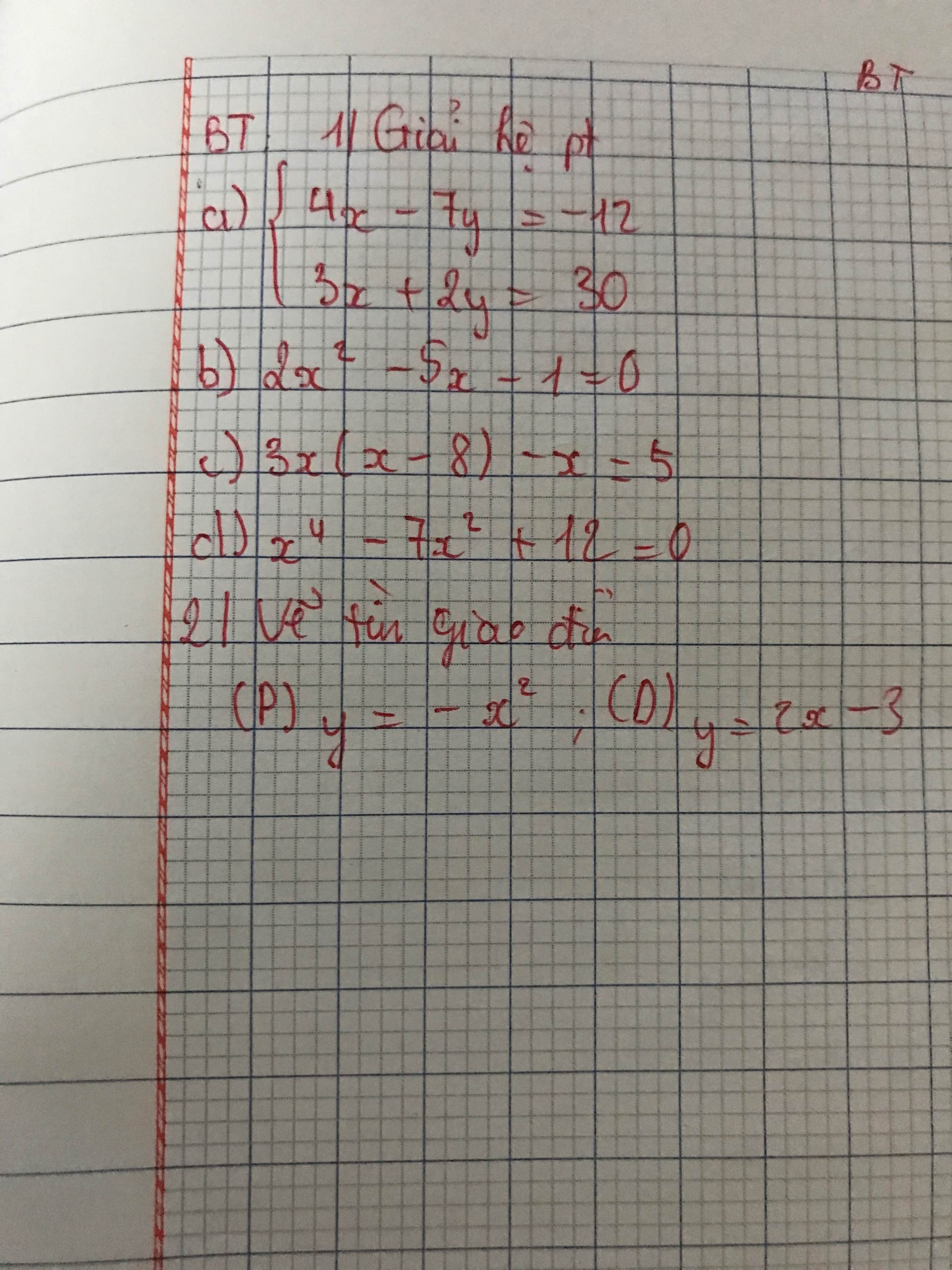\(1,\\ a,\left\{{}\begin{matrix}4x-7y=-12\\3x+2y=30\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}12x-21y=-36\\12x+8y=120\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x-7y=-12\\29y=156\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x-7y=-12\\29y=156\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x-7.\dfrac{456}{29}=-12\\y=\dfrac{156}{29}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{186}{29}\\y=\dfrac{156}{29}\end{matrix}\right.\)
\(b,2x^2-5x-1=0\)
\(\Delta=\left(-5\right)^2-4.2.\left(-1\right)=25+8=33>0\)
\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{33}}{4}\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{33}}{4}\end{matrix}\right.\)
\(c,3x\left(x-8\right)-x=5\\ \Leftrightarrow3x^2-24x-x-5=0\\ \Leftrightarrow3x^2-25x-5=0\)
\(\Delta=\left(-25\right)^2-4.3.\left(-5\right)=625+60=685>0\)
\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{25+\sqrt{685}}{6}\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{25-\sqrt{685}}{6}\end{matrix}\right.\)
\(d,x^4-7x^2+12=0\\ \Leftrightarrow\left(x^4-3x^2\right)-\left(4x^2-12\right)=0\\ \Leftrightarrow x^2\left(x^2-3\right)-4\left(x^2-3\right)=0\\ \Leftrightarrow\left(x^2-3\right)\left(x^2-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\pm\sqrt{3}\\x=\pm2\end{matrix}\right.\)