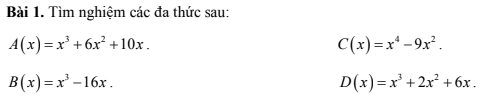Đặt A(x)=0
=>\(x^3+6x^2+10x=0\)
=>\(x\left(x^2+6x+10\right)=0\)
mà \(x^2+6x+10=\left(x^2+6x+9\right)+1=\left(x+3\right)^2+1>0\)
nên x=0
Đặt B(x)=0
=>\(x^3-16x=0\)
=>\(x\left(x^2-16\right)=0\)
=>\(x\left(x-4\right)\left(x+4\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
Đặt C(x)=0
=>\(x^4-9x^2=0\)
=>\(x^2\left(x^2-9\right)=0\)
=>\(x^2\left(x-3\right)\left(x+3\right)=0\)
=>\(\left[{}\begin{matrix}x^2=0\\x-3=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
Đặt D(x)=0
=>\(x^3+2x^2+6x=0\)
=>\(x\left(x^2+2x+6\right)=0\)
mà \(x^2+2x+6=x^2+2x+1+5=\left(x+1\right)^2+5>0\)
nên x=0