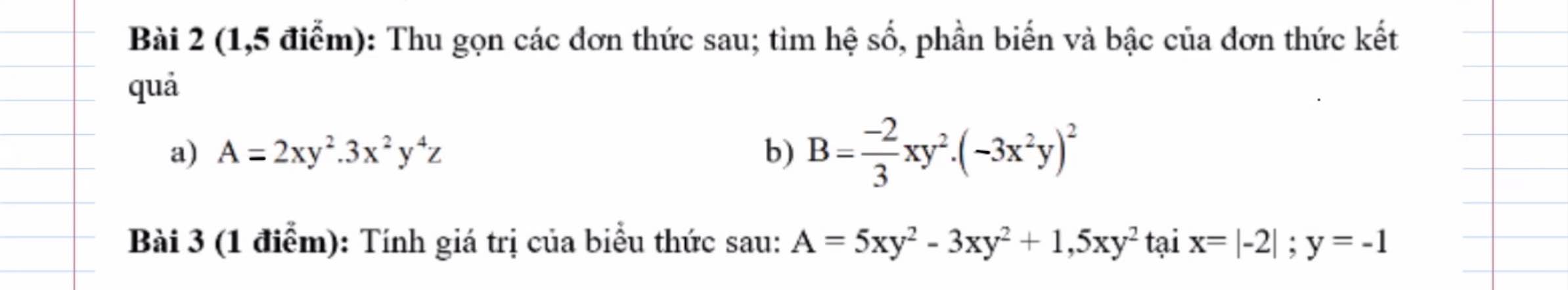Bài 2:
a: \(\left|2x+5\right|-\dfrac{1}{3}=\dfrac{2}{3}\)
=>\(\left|2x+5\right|=\dfrac{2}{3}+\dfrac{1}{3}=1\)
=>\(\left[{}\begin{matrix}2x+5=1\\2x+5=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
b:
ĐKXĐ: x<>-3
\(\dfrac{1.2}{x+3}=\dfrac{5}{4}\)
=>\(x+3=4\cdot\dfrac{1.2}{5}=0,96\)
=>x=0,96-3=-2,04(nhận)
c: \(\dfrac{9}{2}-\left[\dfrac{2}{3}-\left(x+\dfrac{7}{4}\right)\right]=-\dfrac{5}{4}\)
=>\(\dfrac{2}{3}-\left(x+\dfrac{7}{4}\right)=\dfrac{9}{2}+\dfrac{5}{4}=\dfrac{23}{4}\)
=>\(x+\dfrac{7}{4}=\dfrac{2}{3}-\dfrac{23}{4}=\dfrac{8-69}{12}=\dfrac{-61}{12}\)
=>\(x=-\dfrac{61}{12}-\dfrac{7}{4}=-\dfrac{61}{12}-\dfrac{21}{12}=-\dfrac{82}{12}=-\dfrac{41}{6}\)
Bài 3:
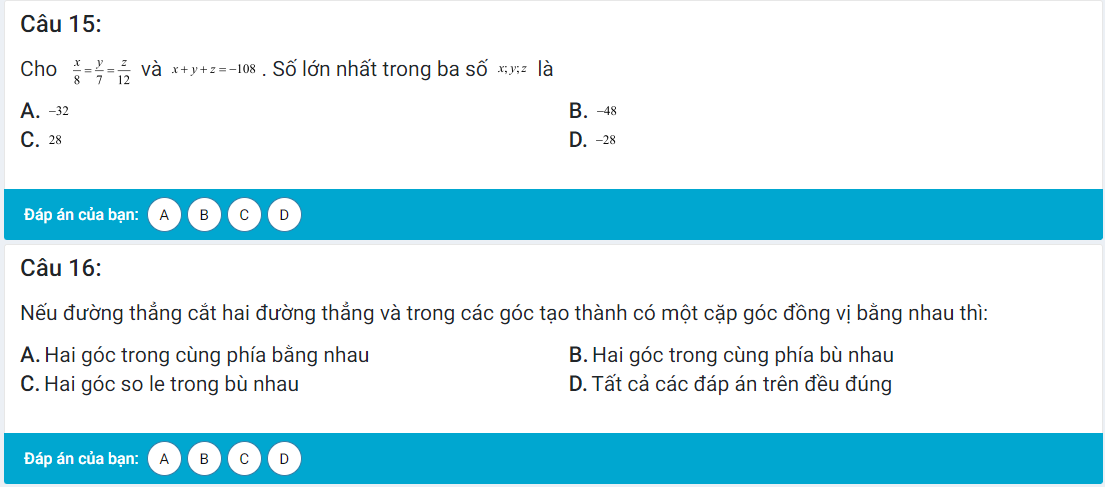
Số lớn là \(12:\dfrac{3}{7}=12\cdot\dfrac{7}{3}=28\)
Câu 5 :
a, Ta có : \(-\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{z}{7};x,y,z\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{5x}{2}\\z=\dfrac{-7x}{2}\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{x-2y+3z}{5x+2y-z}=\dfrac{x-2.\left(-\dfrac{5x}{2}\right)+3.\left(-\dfrac{7x}{2}\right)}{5x+2.\left(-\dfrac{5x}{2}\right)+\dfrac{7x}{2}}=\dfrac{\dfrac{-9x}{2}}{\dfrac{7x}{2}}=-\dfrac{9}{7}\)
\(b,\left(2x-3\right)^{2020}+\left(y-\dfrac{2}{5}\right)^{2022}+\left|x+y-z\right|\le0\)
*Nhận thấy :\(\left\{{}\begin{matrix}\left(2x-3\right)^{2020}\ge0\forall x\\\left(y-\dfrac{2}{5}\right)^{2022}\ge0\forall y\\\left|x+y-z\right|\ge0\forall x,y,z\end{matrix}\right.\)
*Để yêu cầu bài toán được giải quyết thì
\(\left\{{}\begin{matrix}\left(2x-3\right)^{2020}=0\\\left(y-\dfrac{2}{5}\right)^{2022}=0\\x+y-z=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{2}{5}\\z=\dfrac{19}{10}\end{matrix}\right.\)