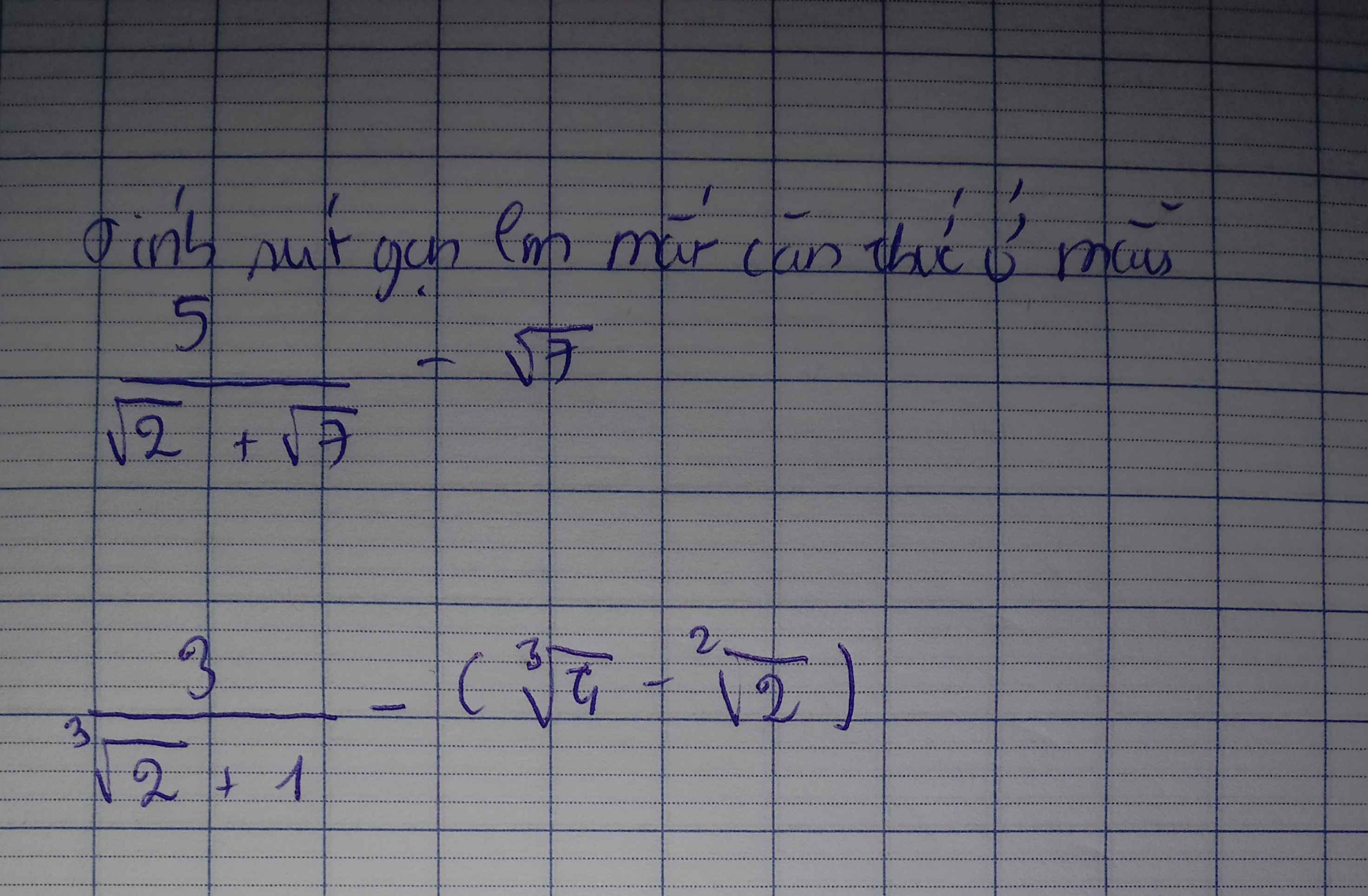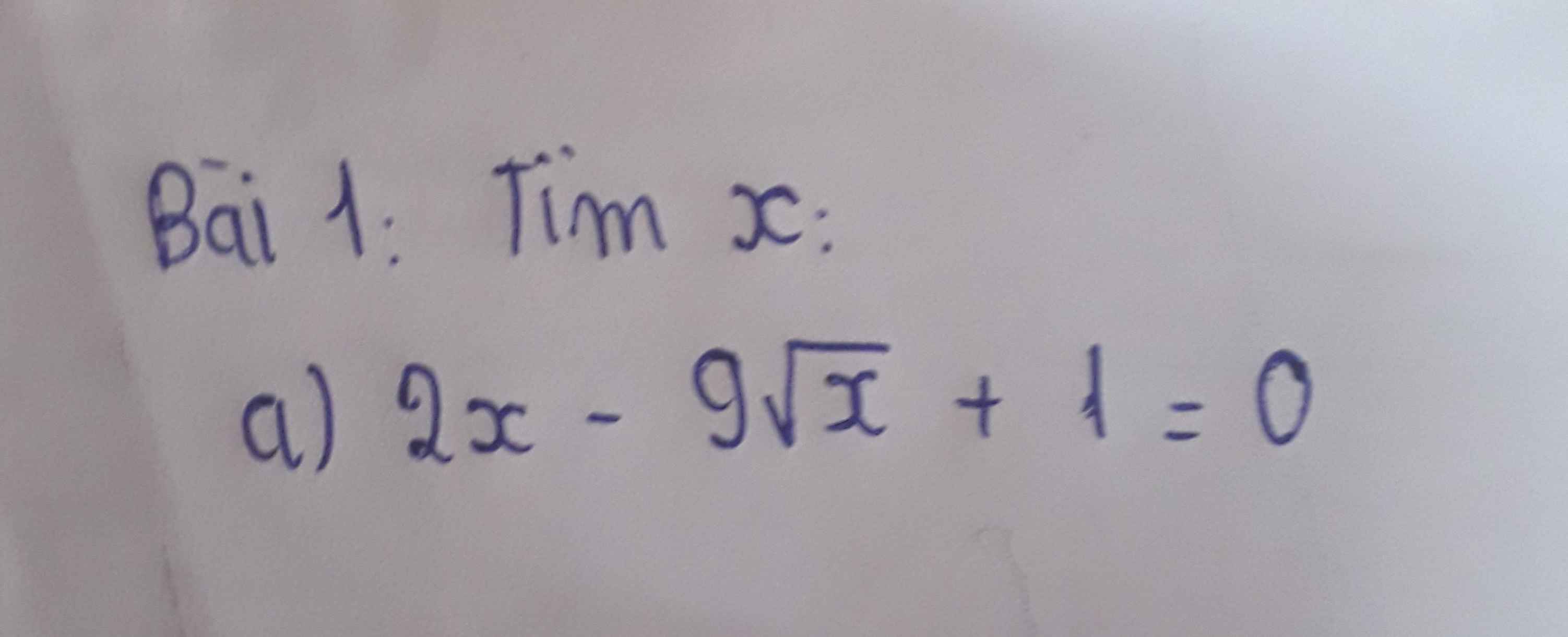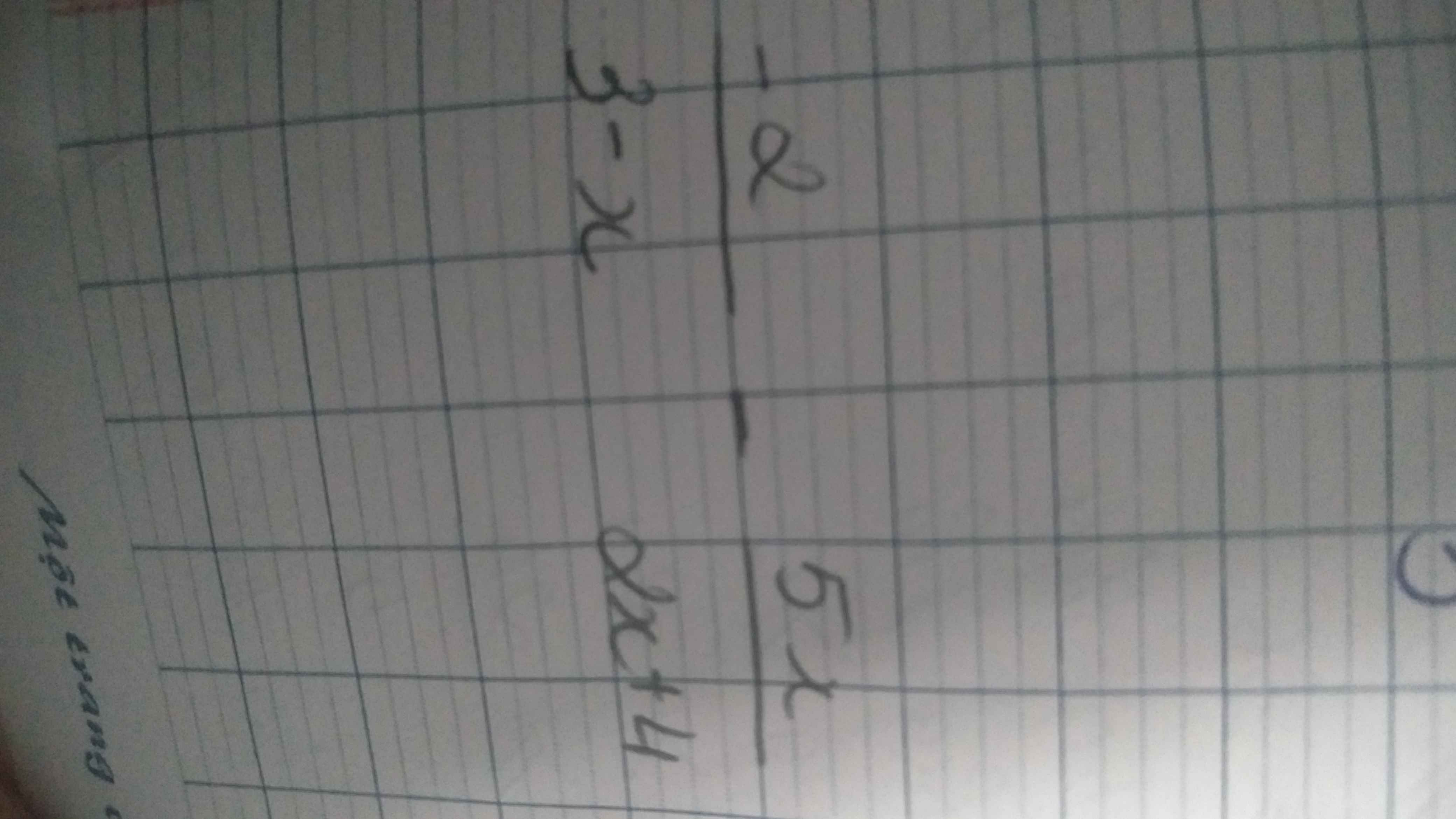1.
\(\sqrt{a}.\sqrt{\frac{32}{a}}=\sqrt{a.\frac{32}{a}}=\sqrt{32}=\sqrt{4^2.2}=4\sqrt{2}\)
2.
\(\sqrt{3,6a}.\sqrt{10a^3}=\sqrt{3,6a.10a^3}=\sqrt{36a^4}=\sqrt{(6a^2)^2}=6a^2\)
3.
\(\sqrt{0,5a}.\sqrt{50a^3}=\sqrt{0,5a.50a^3}=\sqrt{25a^4}=\sqrt{(5a^2)^2}=5a^2\)
4.
\(\sqrt{2a^3}.\sqrt{50a}=\sqrt{2a^3.50a}=\sqrt{100a^4}=\sqrt{(10a^2)^2}=10a^2\)
5.
\(\sqrt{2}.\sqrt{2+\sqrt{3}}=\sqrt{2(2+\sqrt{3})}=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{3+2\sqrt{3}+1}=\sqrt{(\sqrt{3}+1)^2}=\sqrt{3}+1\)
\(\sqrt{2}.\sqrt{2-\sqrt{3}}=\sqrt{2(2-\sqrt{3})}=\sqrt{4-2\sqrt{3}}=\sqrt{3-2\sqrt{3}+1}\)
\(=\sqrt{(\sqrt{3}-1)^2}=|\sqrt{3}-1|=\sqrt{3}-1\)
6.
\(\sqrt{9-\sqrt{17}}.\sqrt{9+\sqrt{17}}=\sqrt{(9-\sqrt{17})(9+\sqrt{17})}\)
\(=\sqrt{9^2-17}=\sqrt{64}=\sqrt{8^2}=8\)
\(\sqrt{\sqrt{17}-\sqrt{8}}.\sqrt{\sqrt{17}+\sqrt{8}}=\sqrt{(\sqrt{17}-\sqrt{8})(\sqrt{17}+\sqrt{8})}\)
\(=\sqrt{17-8}=\sqrt{9}=\sqrt{3^2}=3\)
8.
\(\sqrt{2}(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}})=\sqrt{2(4-\sqrt{7})}-\sqrt{2(4+\sqrt{7})}\)
\(=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}=\sqrt{7-2\sqrt{7}+1}-\sqrt{7+2\sqrt{7}+1}\)
\(=\sqrt{(\sqrt{7}-1)^2}-\sqrt{(\sqrt{7}+1)^2}=|\sqrt{7}-1|-|\sqrt{7}+1|\)
\(=(\sqrt{7}-1)-(\sqrt{7}+1)=-2\)
---------------
\(\sqrt{2}(\sqrt{4,5-2\sqrt{5}}-\sqrt{4,5+2\sqrt{5}})=\sqrt{9-4\sqrt{5}}-\sqrt{9+4\sqrt{5}}\)
\(=\sqrt{2^2-2.2\sqrt{5}+5}-\sqrt{2^2+2.2\sqrt{5}+5}\)
\(=\sqrt{(2-\sqrt{5})^2}-\sqrt{(2+\sqrt{5})^2}=|2-\sqrt{5}|-|2+\sqrt{5}|=-4\)
7.
\(\sqrt{2}(\sqrt{2,5-\sqrt{6}}-\sqrt{2,5+\sqrt{6}})=\sqrt{2(2,5-\sqrt{6})}-\sqrt{2(2,5+\sqrt{6})}\)
\(=\sqrt{5-2\sqrt{6}}-\sqrt{5+2\sqrt{6}}=\sqrt{2-2\sqrt{2.3}+3}-\sqrt{2+2\sqrt{2.3}+3}\)
\(=\sqrt{(\sqrt{2}-\sqrt{3})^2}-\sqrt{(\sqrt{2}+\sqrt{3})^2}\)
\(=|\sqrt{2}-\sqrt{3}|-|\sqrt{2}+\sqrt{3}|=(\sqrt{3}-\sqrt{2})-(\sqrt{2}+\sqrt{3})=-2\sqrt{2}\)
-------------------------------
\(\sqrt{2}(\sqrt{1,5-\sqrt{2}}-\sqrt{1,5+\sqrt{2}})=\sqrt{2(1,5-\sqrt{2})}-\sqrt{2(1,5+\sqrt{2})}\)
\(=\sqrt{3-2\sqrt{2}}-\sqrt{3+2\sqrt{2}}=\sqrt{2-2\sqrt{2}+1}-\sqrt{2+2\sqrt{2}+1}\)
\(=\sqrt{(\sqrt{2}-1)^2}-\sqrt{(\sqrt{2}+1)^2}=|\sqrt{2}-1|-|\sqrt{2}+1|=-2\)
9.
\(\sqrt{2}(\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}})=\sqrt{2(3-\sqrt{5})}-\sqrt{2(3+\sqrt{5})}\)
\(=\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}=\sqrt{5-2\sqrt{5}+1}-\sqrt{5+2\sqrt{5}+1}\)
\(=\sqrt{(\sqrt{5}-1)^2}-\sqrt{(\sqrt{5}+1)^2}=|\sqrt{5}-1|-|\sqrt{5}+1|=-2\)
------------
\(\sqrt{13+30\sqrt{2}+\sqrt{9+4\sqrt{2}}}=\sqrt{13+30\sqrt{2}+\sqrt{(2\sqrt{2})^2+2.2\sqrt{2}+1}}\)
\(=\sqrt{13+30\sqrt{2}+\sqrt{(2\sqrt{2}+1)^2}}=\sqrt{13+30\sqrt{2}+2\sqrt{2}+1}\)
\(=\sqrt{14+32\sqrt{2}}\)
10.
\(\sqrt{6+2\sqrt{5}-\sqrt{13+\sqrt{48}}}=\sqrt{6+2\sqrt{5}-\sqrt{13+4\sqrt{3}}}\)
\(=\sqrt{6+2\sqrt{5}-\sqrt{(2\sqrt{3})^2+2.2\sqrt{3}+1}}\)
\(=\sqrt{6+2\sqrt{5}-\sqrt{(2\sqrt{3}+1)^2}}=\sqrt{6+2\sqrt{5}-(2\sqrt{3}+1)}\)
\(=\sqrt{5+2\sqrt{5}-2\sqrt{3}}\)
11.
$\sqrt{25}+\sqrt{9}=5+3=8$
$\sqrt{25+9}=\sqrt{34}< \sqrt{36}=6< 8$
$\Rightarrow \sqrt{25}+\sqrt{9}>\sqrt{25+9}$
--------------------
$\sqrt{a+b}< \sqrt{a}+\sqrt{b}$
$\Leftrightarrow a+b< (\sqrt{a}+\sqrt{b})^2$
$\Leftrightarrow 0< 2\sqrt{ab}$ (luôn đúng với mọi $a,b>0$)
Vậy ta có đpcm.
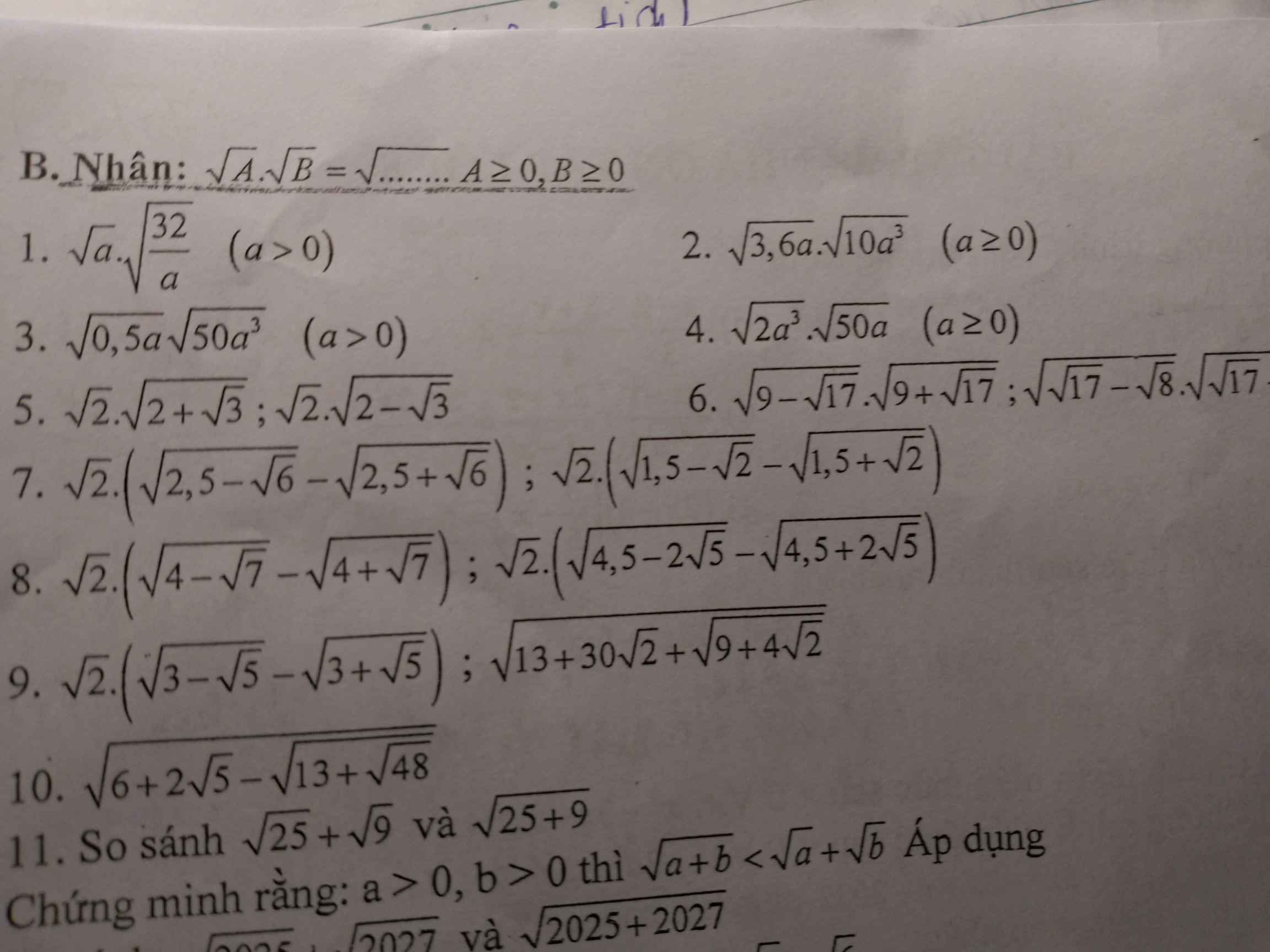

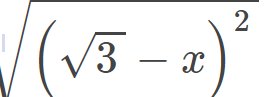
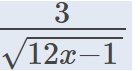 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ