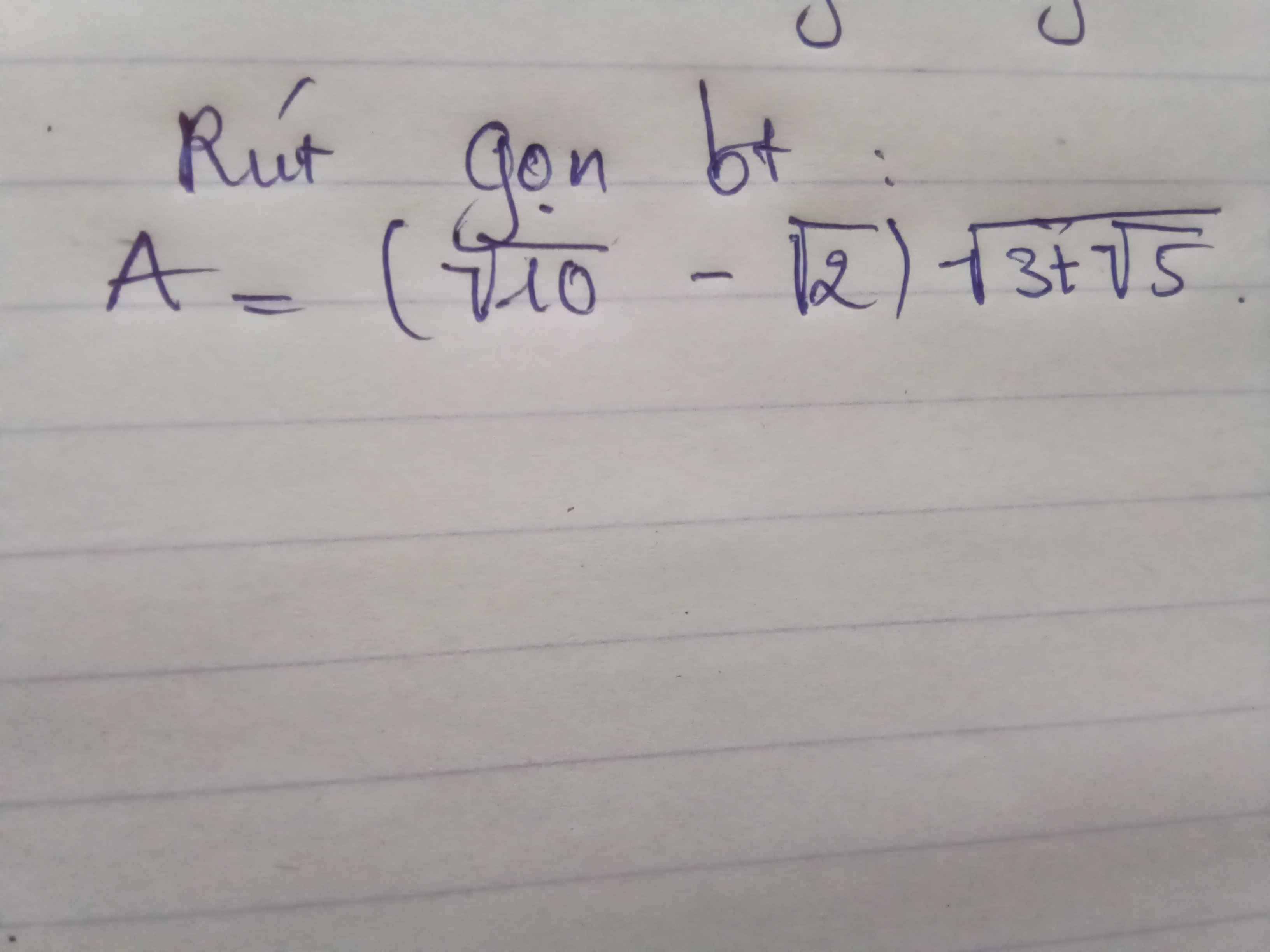Question

Giúp mình với ạ

Answer 1

ta có

A=\(\left(\sqrt{10}-\sqrt{2}\right)\sqrt{3+\sqrt{5}}\)

=\(\sqrt{10}.\sqrt{3+\sqrt{5}}-\sqrt{2}.\sqrt{3+\sqrt{5}}\)

=\(\sqrt{10.\left(3+\sqrt{5}\right)}-\sqrt{2.\left(3+\sqrt{5}\right)}=\sqrt{30+10\sqrt{5}}-\sqrt{6+2\sqrt{5}}\)

=\(\sqrt{5^2+2.5.\sqrt{5}+\left(\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}\right)^2+2.1.\sqrt{5}+1}\)

=\(\sqrt{\left(5+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}=5+\sqrt{5}-\sqrt{5}-1=4\)

Answer 2

Ta có: \(A=\left(\sqrt{10}-\sqrt{2}\right)\sqrt{3+\sqrt{5}}\)

\(=\dfrac{\left(\sqrt{10}-\sqrt{2}\right)\sqrt{6+2\sqrt{5}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}{\sqrt{2}}\)

\(=5-1=4\)