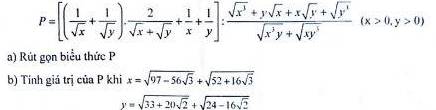a: \(P=\left[\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\right)\cdot\dfrac{2}{\sqrt{x}+\sqrt{y}}+\dfrac{1}{x}+\dfrac{1}{y}\right]:\dfrac{\sqrt{x^3}+y\sqrt{x}+x\sqrt{y}+\sqrt{y^3}}{\sqrt{x^3y}+\sqrt{xy^3}}\)
\(=\left[\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\cdot\dfrac{2}{\sqrt{x}+\sqrt{y}}+\dfrac{x+y}{xy}\right]:\dfrac{x\sqrt{x}+y\sqrt{x}+x\sqrt{y}+y\sqrt{y}}{x\sqrt{xy}+y\sqrt{xy}}\)
\(=\left(\dfrac{2}{\sqrt{xy}}+\dfrac{x+y}{xy}\right):\dfrac{\sqrt{x}\left(x+y\right)+\sqrt{y}\left(x+y\right)}{\sqrt{xy}\left(x+y\right)}\)
\(=\dfrac{x+y+2\sqrt{xy}}{xy}:\dfrac{\left(x+y\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}\left(x+y\right)}\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{xy}\cdot\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\)
b: \(x=\sqrt{97-56\sqrt{3}}+\sqrt{52+16\sqrt{3}}\)
\(=\sqrt{49-2\cdot7\cdot4\sqrt{3}+48}+\sqrt{48+2\cdot4\sqrt{3}\cdot2+4}\)
\(=\sqrt{\left(7-4\sqrt{3}\right)^2}+\sqrt{\left(4\sqrt{3}+2\right)^2}\)
\(=7-4\sqrt{3}+4\sqrt{3}+2=9\)
\(y=\sqrt{33+20\sqrt{2}}+\sqrt{24-16\sqrt{2}}\)
\(=\sqrt{25+2\cdot5\cdot2\sqrt{2}+8}+\sqrt{16-2\cdot4\cdot2\sqrt{2}+8}\)
\(=\sqrt{\left(5+2\sqrt{2}\right)^2}+\sqrt{\left(4-2\sqrt{2}\right)^2}\)
\(=5+2\sqrt{2}+4-2\sqrt{2}=9\)
Khi x=9 và y=9 thì \(P=\dfrac{3+3}{3\cdot3}=\dfrac{6}{9}=\dfrac{2}{3}\)
Giúp mình với ạ, mình cần gấp lắm ạ!
