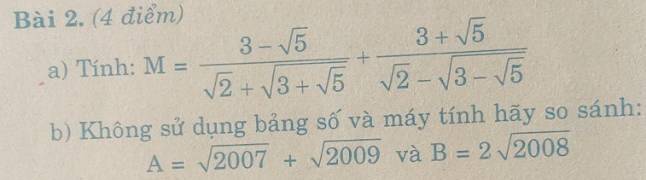a: \(M=\dfrac{3-\sqrt{5}}{\sqrt{2}+\sqrt{3+\sqrt{5}}}+\dfrac{3+\sqrt{5}}{\sqrt{2}-\sqrt{3-\sqrt{5}}}\)
\(=\dfrac{3\sqrt{2}-\sqrt{10}}{2+\sqrt{6+2\sqrt{5}}}+\dfrac{3\sqrt{2}+\sqrt{10}}{2-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{\sqrt{2}\left(3-\sqrt{5}\right)}{2+\sqrt{5}+1}+\dfrac{\sqrt{2}\left(3+\sqrt{5}\right)}{2-\sqrt{5}+1}\)
\(=\dfrac{\sqrt{2}\left(3-\sqrt{5}\right)}{3+\sqrt{5}}+\dfrac{\sqrt{2}\left(3+\sqrt{5}\right)}{3-\sqrt{5}}\)
\(=\dfrac{\sqrt{2}\left(3-\sqrt{5}\right)^2+\sqrt{2}\left(3+\sqrt{5}\right)^2}{9-5}\)
\(=\dfrac{\sqrt{2}\left(14-6\sqrt{5}+14+6\sqrt{5}\right)}{4}=\sqrt{2}\cdot\dfrac{28}{4}=7\sqrt{2}\)
b: \(A^2=\left(\sqrt{2007}+\sqrt{2009}\right)^2=4016+2\cdot\sqrt{2007\cdot2009}\)
=>\(A^2=4016+2\cdot\sqrt{2008^2-1}\)
\(B^2=\left(2\sqrt{2008}\right)^2=4\cdot2008=2016+2\cdot\sqrt{2018^2}\)
2018^2>2018^2-1
=>\(2\cdot\sqrt{2008^2}>2\cdot\sqrt{2008^2-1}\)
=>\(A^2< B^2\)
=>A<B
Giúp mình với ạ, mình cần gấp lắm ạ!
