Giúp mình giải câu c và d với ạ:
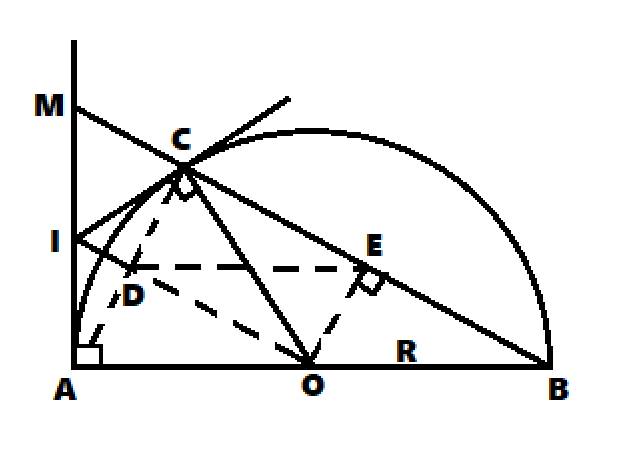
Gọi C là một điểm bất kì trên nửa đường tròn \((O)\), đường kính AB \(=\) R \(\left(C\ne A,C\ne B\right)\). Tia BC cắt tiếp tuyến tại A của nửa đường tròn tại M. Tiếp tuyến tại C của nửa đường tròn cắt AM tại I.
a, Chứng minh bốn điểm I, A, O, C cùng thuộc một đường tròn
b, Chứng minh OI \(\perp\) AC
c, Gọi D là giao điểm của OI và Ac. Vẽ OE vuông góc với BC \(\left(E\varepsilon BC\right)\). Chứng minh DE \(=\) R
d, Chứng minh IC\(^2\) \(=\) \(\dfrac{1}{4}\) MC . MB
a: Xét tứ giác IAOC có
\(\widehat{IAO}+\widehat{ICO}=90^0+90^0=180^0\)
=>IAOC là tứ giác nội tiếp
=>I,A,O,C cùng thuộc một đường tròn
b: Xét (O) có
IA,IC là tiếp tuyến
Do đó: IA=IC
=>I nằm trên đường trung trực của AC(1)
ta có: OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra OI là đường trung trực của AC
=>OI\(\perp\)AC
c: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Ta có: OI là đường trung trực của AC
=>OI vuông góc với AC tại trung điểm của AC
mà OI cắt AC tại D
nên OI\(\perp\)AC tại D và D là trung điểm của AC
Xét tứ giác CDOE có
\(\widehat{CDO}=\widehat{CEO}=\widehat{ECD}=90^0\)
=>CDOE là hình chữ nhật
=>CO=DE=R
d: Xét ΔIAC có IA=IC
nên ΔIAC cân tại I
=>\(\widehat{IAC}=\widehat{ICA}\)
Ta có: ΔACB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)MB tại C
=>ΔACM vuông tại C
Ta có: \(\widehat{IAC}+\widehat{IMC}=90^0\)(ΔACM vuông tại C)
\(\widehat{ICA}+\widehat{ICM}=\widehat{ACM}=90^0\)
mà \(\widehat{IAC}=\widehat{ICA}\)
nên \(\widehat{IMC}=\widehat{ICM}\)
=>IM=IC
mà IC=IA
nên IM=IA
=>I là trung điểm của MA
=>\(MA=2\cdot IC\)
Xét ΔABM vuông tại A có AC là đường cao
nên \(MC\cdot MB=MA^2\)
=>\(MC\cdot MB=\left(2\cdot IC\right)^2=4\cdot IC^2\)
=>\(IC^2=\dfrac{1}{4}\cdot MC\cdot MB\)

