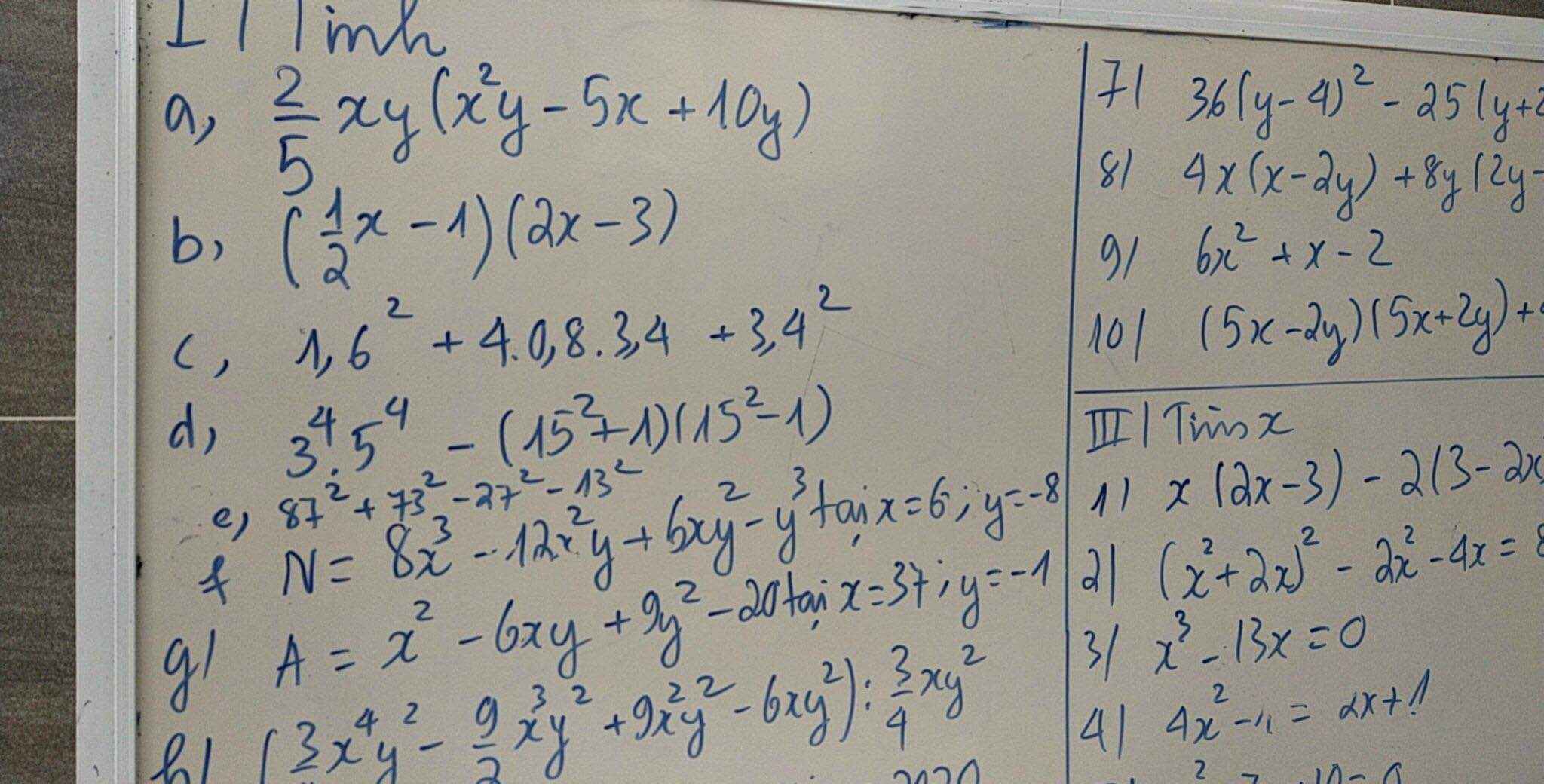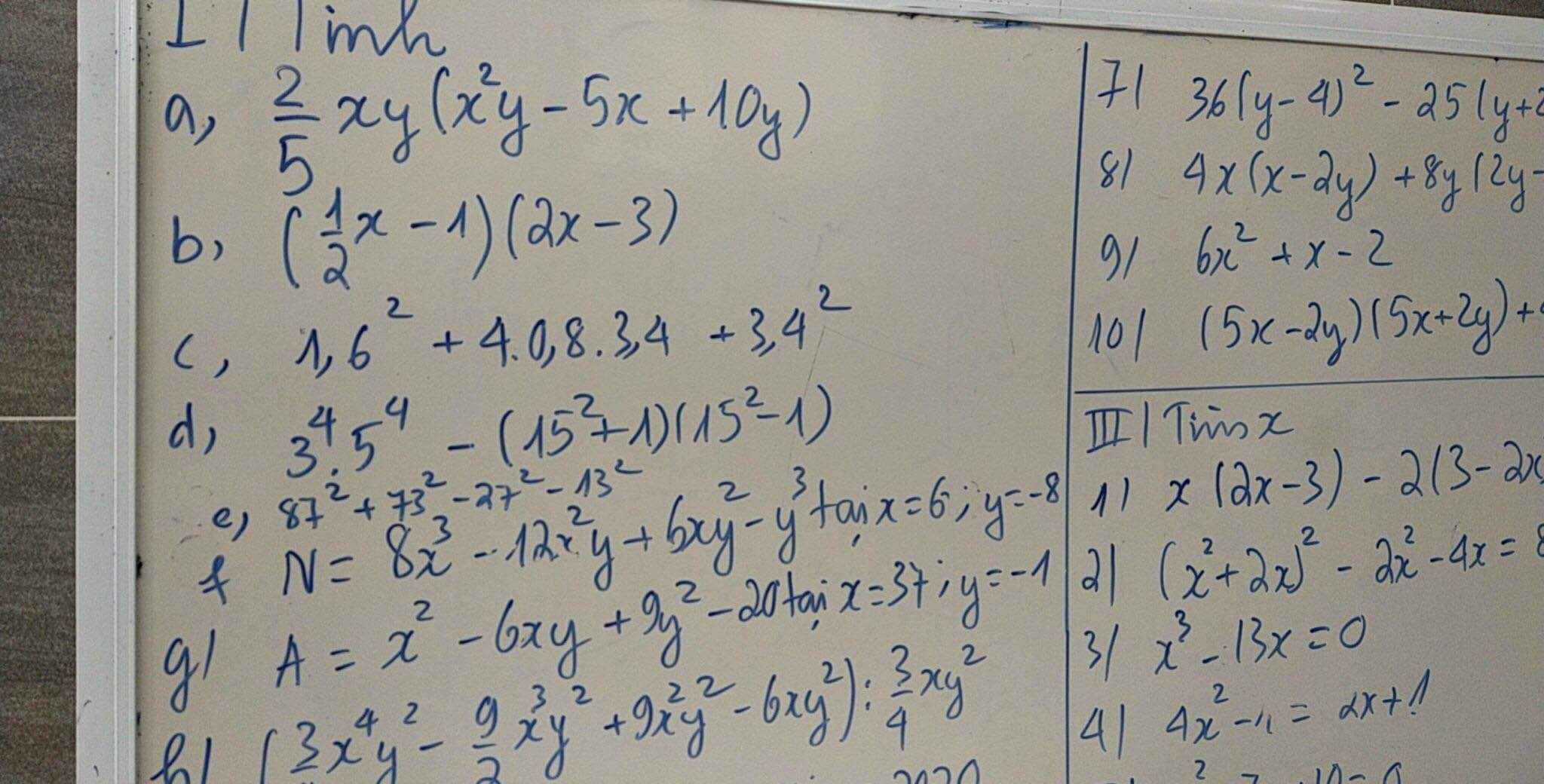II:
1: =x^4-x^2-4x^2+4=(x^2-1)(x^2-4)=(x-1)(x+1)(x-2)(x+2)
2:=x^2(x-3)-4(x-3)=(x-3)(x^2-4)
=(x-3)(x-2)(x+2)
3:=(x+y+z-x)[(x+y+z)^2+x(x+y+z)+x^2]-(y+z)(y^2-yz+z^2)
=(y+z)[(x+y+z)^2+x(x+y+z)+x^2-y^2+yz-z^2]
=(y+z)(x^2+y^2+z^2+2xy+2yz+2xz+x^2+xy+xz+x^2-y^2-z^2+yz]
=(y+z)(3x^2+3xy+3xz+3yz)
=(y+z)*3*(x^2+xy+xz+yz)
=(y+z)(x+y)(x+z)*3
5:=x(x+y)-5(x+y)=(x+y)(x-5)