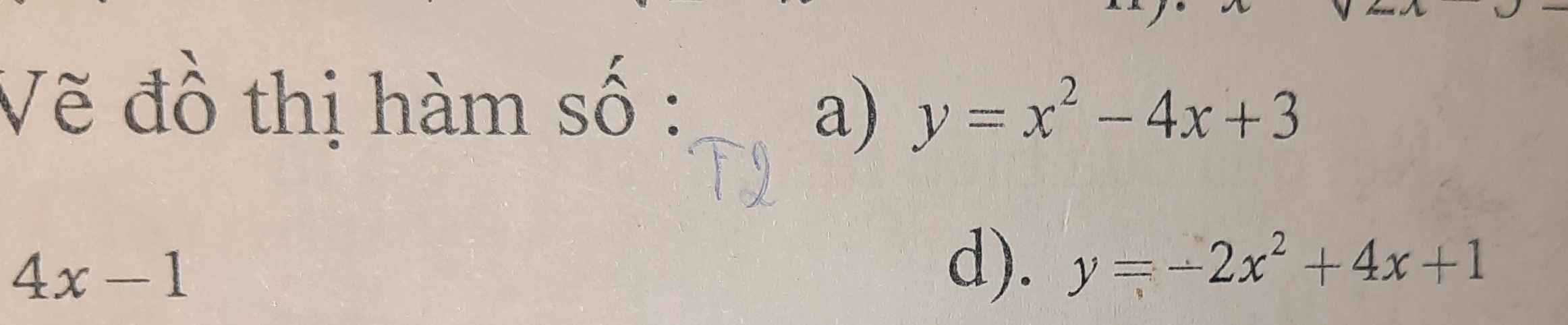\(\overrightarrow{u}=4\overrightarrow{MA}-3\left(\overrightarrow{MA}+\overrightarrow{AB}\right)+\overrightarrow{MA}+\overrightarrow{AC}-2\left(\overrightarrow{MA}+\overrightarrow{AD}\right)\)
\(=-3\overrightarrow{AB}+\overrightarrow{AC}-2\overrightarrow{AD}=-3\left(\overrightarrow{AB}+\overrightarrow{AD}\right)+\overrightarrow{AC}+\overrightarrow{AD}\)
\(=-3\overrightarrow{AC}+\overrightarrow{AC}+\overrightarrow{AD}=-2\overrightarrow{AC}+\overrightarrow{AD}\)
\(\overrightarrow{u}^2=\left(-2\overrightarrow{AC}+\overrightarrow{AD}\right)^2=4AC^2-4\overrightarrow{AC}.\overrightarrow{AD}+AD^2\)
\(=4\left(a\sqrt{2}\right)^2-4.a\sqrt{2}.a.cos45^0+a^2=5a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=a\sqrt{5}\)
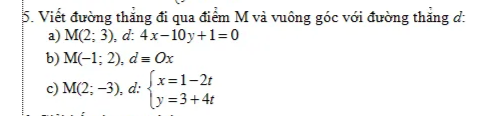
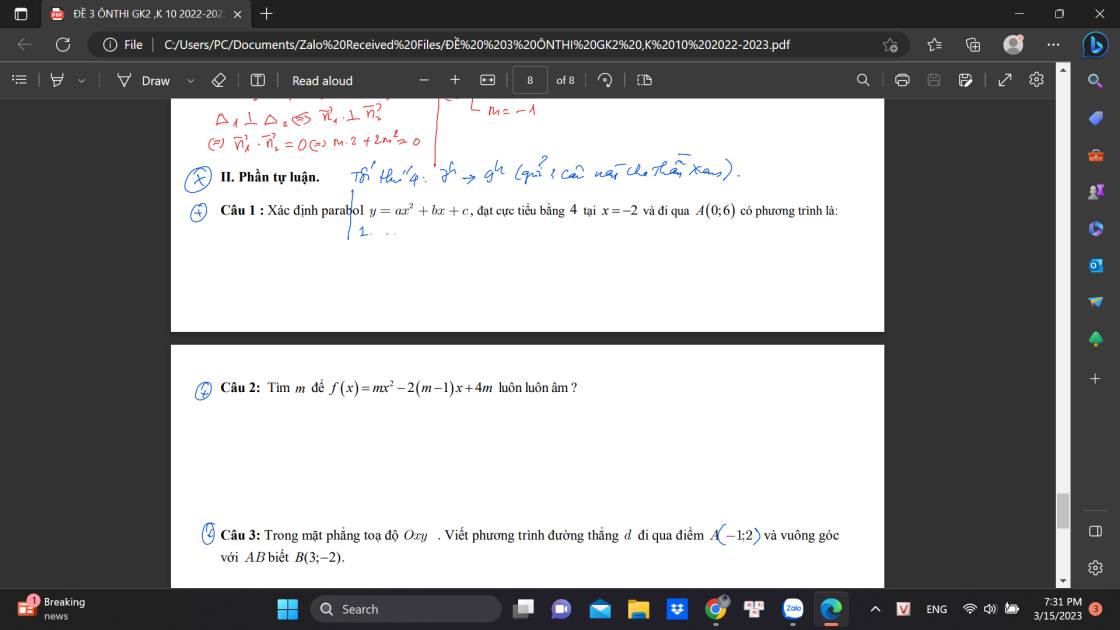
giúp mình mấy câu này với mình cảm ơn nhìu ạ