5.
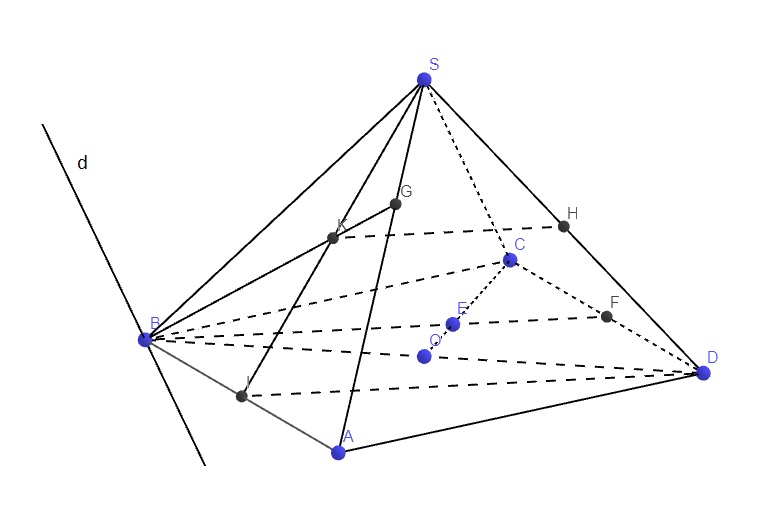
Do H là trung điểm SD, K là trung điểm SI
\(\Rightarrow\) HK là đường trung bình tam giác SDI
\(\Rightarrow HK||ID\) (1)
\(\Rightarrow HK||\left(ABCD\right)\)
Gọi F là trung điểm CD \(\Rightarrow\)E thuộc BF và tứ giác BFDI là hình bình hành (cặp cạnh đối BI, CF song song và bằng nhau)
\(\Rightarrow BF||ID\) (2)
(1);(2) \(\Rightarrow BF\subset\left(HKE\right)\)
Trong mp (SAB), nối BK kéo dài cắt SA tại G
\(\Rightarrow\) Tứ giác AGHF là thiết diện của (HKE) và chóp
b.
Ta có HF là đường trung bình của tam giác SCD
\(\Rightarrow HF||SC\)
\(\Rightarrow\) Giao tuyến của 2 mp (HKE) và (SBC) song song HF và SC
Lại có B là 1 điểm chung của 2 mp
\(\Rightarrow\) Qua B kẻ đường thẳng d song song SC thì d là giao tuyến của (HKE) và (SBC)
3.
Thay vì khai triển nhị thức và đồng nhất hệ số rất phức tạp, những bài này thường được chứng minh bằng phương pháp chọn như sau:
Giả sử một nhóm có 100 em học sinh, trong đó có 70 nam và 30 nữ. Hỏi có bao nhiêu cách chọn ra 12 em để lập 1 đội văn nghệ?
Phương pháp chọn thứ nhất: chọn 12 em từ 100 em có \(C_{100}^{12}\) cách
Phương pháp chọn thứ hai: ta chọn theo các trường hợp tỉ mỉ hơn như sau:
- Nếu 12 bạn chỉ toàn nam: có \(C_{30}^0.C_{70}^{12}\) cách
- Nếu 12 bạn có 1 nữ và 11 nam: có \(C_{30}^1C_{70}^{11}\) cách
- Nếu 12 bạn có 2 nữ và 10 nam: \(C_{30}^2C_{70}^{10}\) cách
...
- Nếu 12 bạn chỉ toàn nữ: \(C_{30}^{12}C_{70}^0\) cách
Vậy theo phương pháp thứ hai, ta có: \(C_{30}^0C_{70}^{12}+C_{30}^1C_{70}^{11}+...+C_{30}^{12}C_{70}^0\) cách
Dù chọn theo phương pháp nào thì số cách chọn cũng giống nhau, vì thế ta được:
\(C_{100}^{12}=C_{30}^0C_{70}^{12}+C_{30}^1C_{70}^{11}+...+C_{30}^{12}C_{70}^0\)
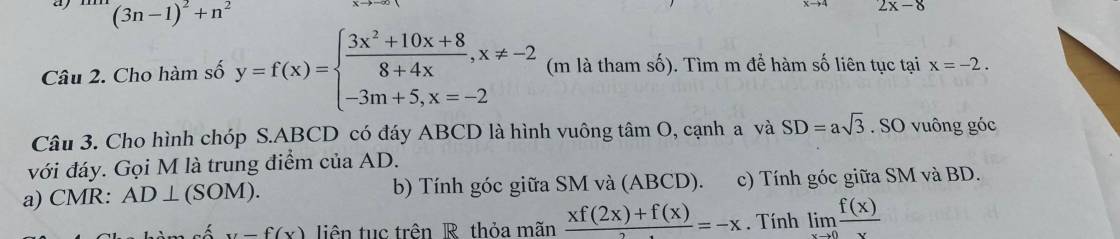
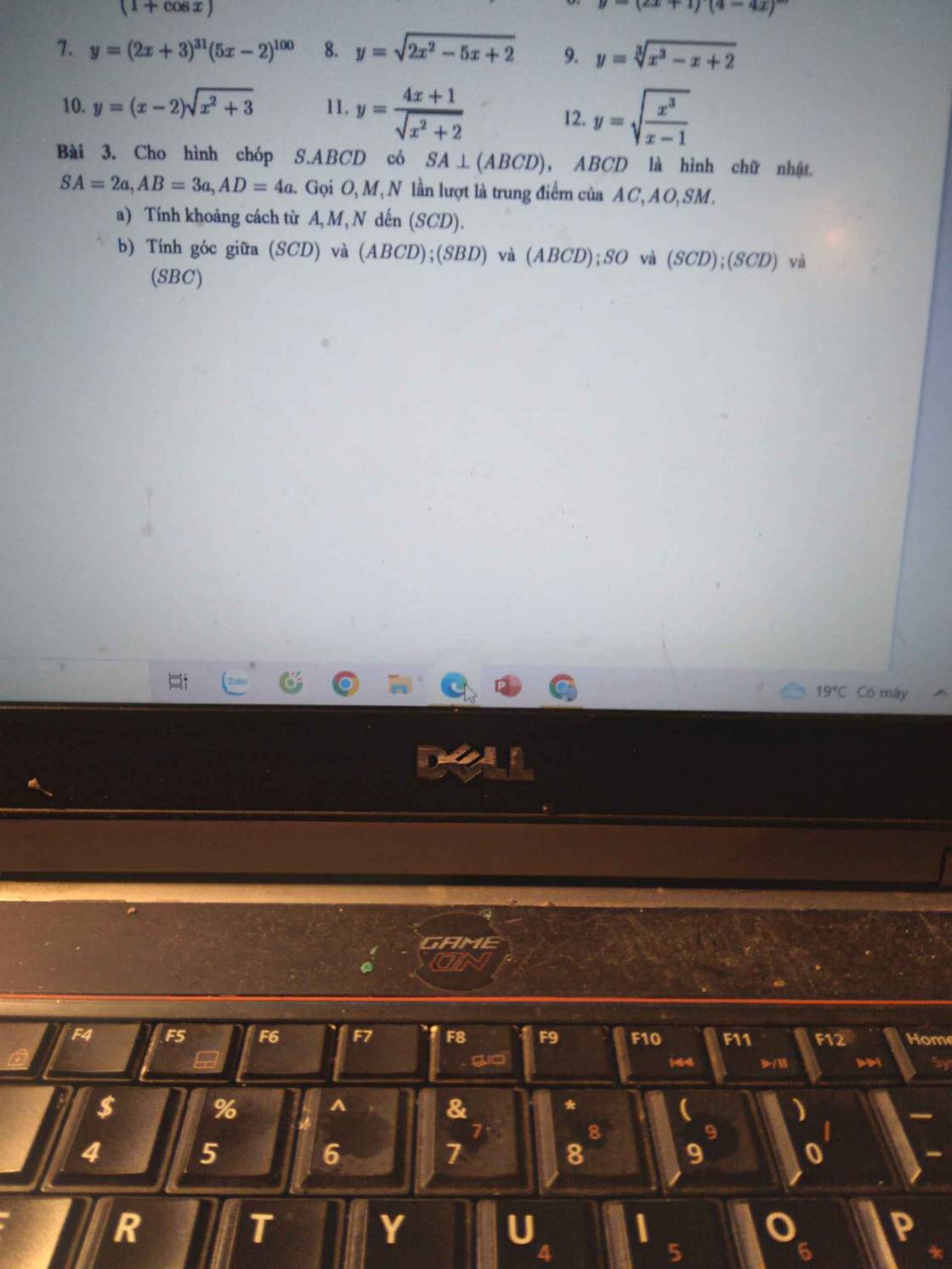Giúp em bài 3 với ạ. Em cảm ơn ạ