\(x^2-3x-1=0\)
Theo vi-ét: \(\left\{{}\begin{matrix}x_1x_2=-1\\x_1+x_2=3\end{matrix}\right.\)
\(A=\dfrac{x_1}{x_1-2x_2}+\dfrac{x_2}{x_2-2x_1}\)
\(=\dfrac{x_1\left(x_2-2x_1\right)}{\left(x_1-2x_2\right)\left(x_2-2x_1\right)}+\dfrac{x_2\left(x_1-2x_2\right)}{\left(x_1-2x_2\right)\left(x_2-2x_1\right)}\)
\(=\dfrac{x_1\left(x_2-2x_1\right)+x_2\left(x_1-2x_2\right)}{\left(x_1-2x_2\right)\left(x_2-2x_1\right)}\)
\(=\dfrac{x_1x_2-2x_1^2+x_1x_2-2x_2^2}{x_1x_2-2x_1^2-2x_2^2+4x_1x_2}\)
\(=\dfrac{2x_1x_2-2\left(x_1^2+x_2^2\right)}{5x_1x_2-2\left(x_1^2+x_2^2\right)}\)
\(=\dfrac{2x_1x_2-2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}{5x_1x_2-2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}\)
\(=\dfrac{2x_1x_2-2\left(x_1+x_2\right)^2+4x_1x_2}{5x_1x_2-2\left(x_1+x_2\right)^2+4x_1x_2}\)
\(=\dfrac{6x_1x_2-2\left(x_1+x_2\right)^2}{9x_1x_2-2\left(x_1+x_2\right)^2}\)
\(=\dfrac{6\cdot\left(-1\right)-2\cdot3^2}{9\cdot\left(-1\right)-2\cdot3^2}\)
\(=\dfrac{-6-18}{-9-18}\)
\(=\dfrac{8}{9}\)




 giúp mình câu c bài 2
giúp mình câu c bài 2


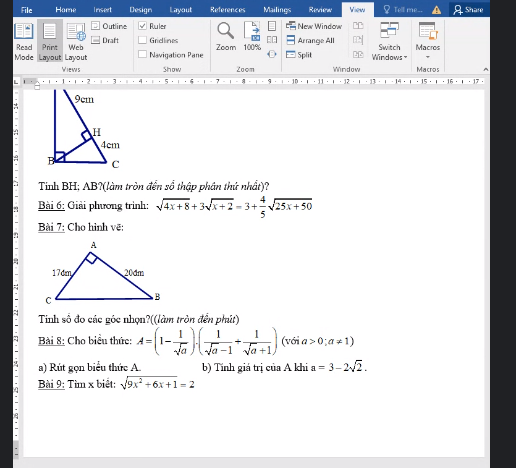 giúp em bài 8 với 9 ạ :<
giúp em bài 8 với 9 ạ :<
