\(\Delta PBE\) (hình như có j đó sai sai ak)
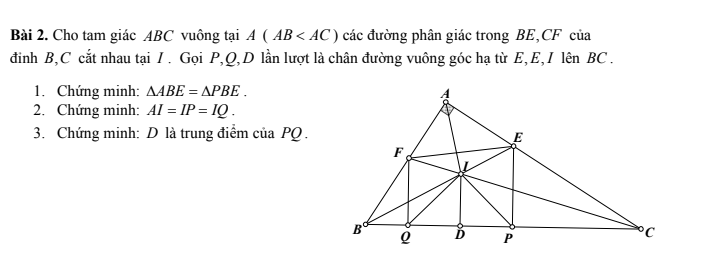
1. Xét \(\Delta ABEvà\Delta PBEcó:\)
\(\widehat{EAB}=\widehat{EPB}\left(=90^o\right)\)
Chung BE
\(\widehat{ABE}=\widehat{PBE}\) (BE là phân giác \(\widehat{ABC}\))
\(\Rightarrow\Delta ABE=\Delta PBE\) (c.g.c)
2. \(\Delta ABE=\Delta PBE\)(cmb)
\(\Rightarrow AB=PB\)(2 cạnh tương ứng)
Xét \(\Delta ABI\) và \(\Delta PBI\) có:
\(AB=PB\left(cmt\right)\)
\(\widehat{ABI}=\widehat{PBI}\)(gt)
chung BI
\(\Rightarrow\Delta ABI=\Delta PBI\)(c.g.c)
\(\Rightarrow IA=IP\) (2 cạnh tương ứng) (1)
Xét \(\Delta CQF\) và \(\Delta CAF\) có:
\(\widehat{CQF}=\widehat{CAF}\left(=90^o\right)\)
Chung CF
\(\widehat{FCQ}=\widehat{FCA}\)(gt)
\(\Rightarrow\Delta CQF=\Delta CAF\)(ch-gn)
\(\Rightarrow CQ=CA\)(2 cạnh tương ứng)
Xét \(\Delta ICQ\) và \(\Delta ICA\) có:
Chung IC
\(\widehat{ICQ}=\widehat{ICA}\)(gt)
\(CQ=CA\)(cmt)
\(\Rightarrow\) \(\Delta ICQ\) \(=\) \(\Delta ICA\) (c.g.c)
\(\Rightarrow IQ=IA\)(2 cạnh tương ứng) (2)
Từ (1), (2) \(\Rightarrow AI=IP=IQ\)
3. \(IQ=IP\Rightarrow\Delta IQP\) cân tại I
Vì trong tam giác cân, đường cao đồng thời là đường trung tuyến mà ID là đường là đường trung tuyến trong tam giác cân IQP⇒ID là đường trung tuyến trong tam giác IQP⇒QD=DP