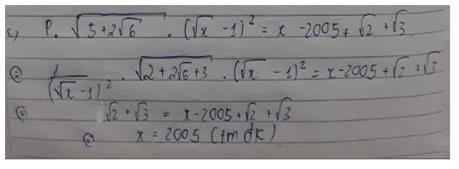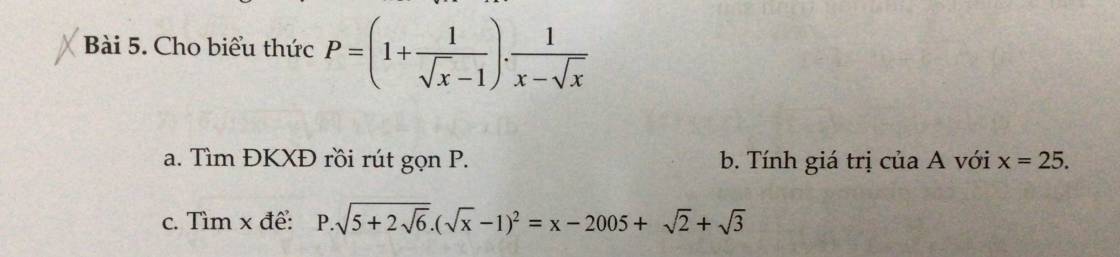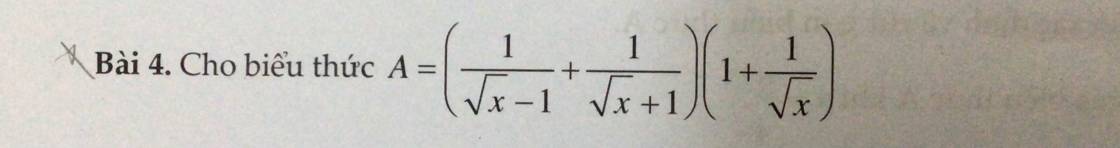a: ĐKXĐ: x>0; x<>1
\(P=\dfrac{\sqrt{x}-1+1}{\sqrt{x}-1}\cdot\dfrac{1}{x-\sqrt{x}}=\dfrac{1}{\left(\sqrt{x}-1\right)^2}\)
b: Khi x=25 thì A=1/(5-1)^2=1/16
c: \(P\cdot\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{x}-1\right)^2=x-2005+\sqrt{2}+\sqrt{3}\)
=>\(\sqrt{3}+\sqrt{2}=x-2005+\sqrt{2}+\sqrt{3}\)
=>x=2005
a. ĐKXĐ: \(x\ne1,x>0\)
\(P=\dfrac{\sqrt{x}-1+1}{\sqrt{x}-1}.\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{1}{\left(\sqrt{x}-1\right)^2}\)
b
Khi x = 25
\(P=\dfrac{1}{\left(\sqrt{25}-1\right)^2}=\dfrac{1}{4^2}=\dfrac{1}{16}\)