a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>BDEC là hình thang
mà góc B=góc C
nên BDEC là hình thang cân
b: góc ABC=góc ACB=(180-70)/2=55 độ
góc BDE=góc DEC=180-55=125 độ
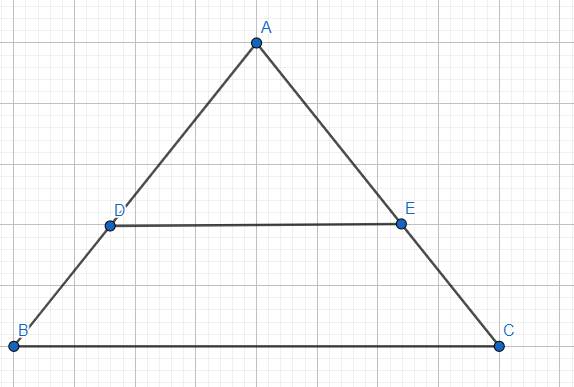
a)xét tam giác abc có
ab=ac suy ra tam giác abc cân tại a
=> \(b=\dfrac{180^o-a}{2}\left(đl\right)\) (1)
xét tam giác ade có
ad=ae suy ra tam giác ade cân tại a
=> \(d_2=\dfrac{180^o-a}{2}\left(đl\right)\) (2)
từ (1) , (2) suy ra \(b=d_2\)
mà 2 góc này ở vị đồng vị suy ra de//bc
xét từ giác debc có
de//bc(cmt) suy ra debc là hình thang
có abc là tam giác cân(cmt)
=> góc b=c
xét hình thang debc có
b=c(cmt) suy ra debc là hình thang cân
b)
xét hình thang cân debc có
\(B=C=\dfrac{180^o-A}{2}=55^o\)
Có de//bc nên \(B+D_1=180^o\left(TCP\right)=>D_1=125^o\)
Có de//bc nên \(C+E_1=180^o\left(TCP\right)=>E_1=125^o\)


