Bài 4:
a: \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
b: \(x+5\sqrt{x}+6=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)
c: \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
d: \(3x-6\sqrt{x}-6=3\left(x-\sqrt{x}-2\right)=3\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
Bài 3:
a) \(\sqrt{3\left(x+2\right)}=6\left(đk:x\ge-2\right)\)
\(\Leftrightarrow3\left(x+2\right)=36\)
\(\Leftrightarrow3x=30\Leftrightarrow x=10\)(thỏa đk)
b) \(\sqrt{5x^2}=x+2\left(đk:x\ge-2\right)\)
\(\Leftrightarrow5x^2=\left(x+2\right)^2\)
\(\Leftrightarrow4x^2-4x-4=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=\dfrac{5}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{\sqrt{5}}{2}\\x-\dfrac{1}{2}=-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt{5}}{2}\\x=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)(thỏa đk)
c) \(\sqrt{x^2-8x+16}=x+2\left(1\right)\left(đk:x\ge-2\right)\)
\(\Leftrightarrow\sqrt{\left(x-4\right)^2}=x+2\Leftrightarrow\left|x-4\right|=x+2\)
TH1: \(x\ge4\)
\(\left(1\right)\Leftrightarrow x-4=x+2\Leftrightarrow-4=2\)(vô lý)
TH2: \(-2\le x< 4\)
\(\left(1\right)\Leftrightarrow4-x=x+2\)
\(\Leftrightarrow x=1\)(thỏa đk)
d) \(\sqrt{x^2-4x+4}-2x+5=0\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}-2x+5=0\left(2\right)\Leftrightarrow\left|x-2\right|-2x+5=0\)
TH1: \(x\ge2\)
\(\left(2\right)\Leftrightarrow x-2-2x+5=0\)
\(\Leftrightarrow x=3\)(thỏa đk)
TH2: \(\dfrac{5}{2}\le x< 2\)
\(\left(2\right)\Leftrightarrow2-x-2x+5=0\)
\(\Leftrightarrow x=\dfrac{7}{3}\)(không thỏa đk)
Bài 4:
a) \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
b) \(x+5\sqrt{x}+6=\left(\sqrt{x}+\dfrac{5}{2}\right)^2-\dfrac{1}{4}=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)
c) \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
d) \(3x-6\sqrt{x}-6=3\left(\sqrt{x}-1-\sqrt{3}\right)\left(\sqrt{x}-1+\sqrt{3}\right)\)
Bài 3:
a: Ta có: \(\sqrt{3\left(x+2\right)}=6\)
\(\Leftrightarrow3\left(x+2\right)=36\)
\(\Leftrightarrow x+2=12\)
hay x=10
b: Ta có: \(\sqrt{5x^2}=x+2\)
\(\Leftrightarrow5x^2=x^2-4x+4\)
\(\Leftrightarrow4x^2+4x-4=0\)
\(\Leftrightarrow x^2+x-1=0\)
\(\text{Δ}=1^2-4\cdot1\cdot\left(-1\right)=5\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-1-\sqrt{5}}{2}\left(nhận\right)\\x_2=\dfrac{-1+\sqrt{5}}{2}\left(nhận\right)\end{matrix}\right.\)
c: Ta có: \(\sqrt{x^2-8x+16}=x+2\)
\(\Leftrightarrow\left|x-4\right|=x+2\)
\(\Leftrightarrow4-x=x+2\left(x< 4\right)\)
\(\Leftrightarrow-2x=-2\)
hay x=1(nhận)
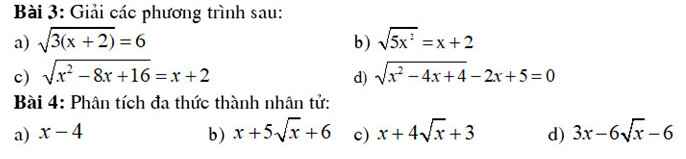








 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ


