Bài 1:
b: \(\left(2x-1\right)^2-\left(x+3\right)^2=0\)
=>(2x-1-x-3)(2x-1+x+3)=0
=>(x-4)(3x+2)=0
=>\(\left[{}\begin{matrix}x-4=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)
c: \(4x^2-1+\left(1-2x\right)\left(x+11\right)=0\)
=>\(\left(2x-1\right)\left(2x+1\right)-\left(2x-1\right)\left(x+11\right)=0\)
=>(2x-1)(2x+1-x-11)=0
=>(2x-1)(x-10)=0
=>\(\left[{}\begin{matrix}2x-1=0\\x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=10\end{matrix}\right.\)
a: \(\left(2x-1\right)\cdot x^2+9\left(1-2x\right)=0\)
=>\(\left(2x-1\right)\left(x^2-9\right)=0\)
=>(2x-1)(x-3)(x+3)=0
=>\(\left[{}\begin{matrix}2x-1=0\\x-3=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=3\\x=-3\end{matrix}\right.\)
f: \(\left(x-5\right)\left(6x+3\right)=\left(2x-7\right)\left(3x+5\right)\)
=>\(6x^2+3x-30x-15=6x^2+10x-21x-35\)
=>-27x-15=-11x-35
=>-27x+11x=-35+15
=>-16x=-20
=>\(x=\dfrac{5}{4}\left(nhận\right)\)
e: \(\dfrac{x+4}{5}-x-5=\dfrac{x+3}{3}-\dfrac{x-2}{2}\)
=>\(\dfrac{x+4+5\left(-x-5\right)}{5}=\dfrac{2\cdot\left(x+3\right)-3\left(x-2\right)}{6}\)
=>\(\dfrac{x+4-5x-25}{5}=\dfrac{2x+6-3x+6}{6}\)
=>\(\dfrac{-4x-21}{5}=\dfrac{-x+12}{6}\)
=>\(\dfrac{4x+21}{5}=\dfrac{x-12}{6}\)
=>6(4x+21)=5(x-12)
=>24x+126=5x-60
=>19x=-186
=>\(x=-\dfrac{186}{19}\)
d: \(3x^2-7x+4=0\)
=>\(3x^2-3x-4x+4=0\)
=>3x(x-1)-4(x-1)=0
=>(x-1)(3x-4)=0
=>\(\left[{}\begin{matrix}x-1=0\\3x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{3}\end{matrix}\right.\)
i: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x-1}{x^2-4}=\dfrac{3}{2-x}\)
=>\(\dfrac{x-1}{\left(x-2\right)\left(x+2\right)}=\dfrac{-3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
=>x-1=-3(x+2)=-3x-6
=>4x=-5
=>\(x=-\dfrac{5}{4}\left(nhận\right)\)
h: \(\dfrac{x+4}{5}+\dfrac{3x+2}{10}=\dfrac{x-1}{3}\)
=>\(\dfrac{6\left(x+4\right)+3\left(3x+2\right)}{30}=\dfrac{10\left(x-1\right)}{30}\)
=>6(x+4)+3(3x+2)=10(x-1)
=>6x+24+9x+6=10x-10
=>15x+30=10x-10
=>5x=-40
=>x=-8
g: \(\dfrac{x+4}{5}-2x+1=\dfrac{x}{3}-\dfrac{2-x}{6}\)
=>\(\dfrac{x+4+5\left(-2x+1\right)}{5}=\dfrac{2x-2+x}{6}\)
=>\(\dfrac{x+4-10x+5}{5}=\dfrac{3x-2}{6}\)
=>\(\dfrac{-9x+9}{5}=\dfrac{3x-2}{6}\)
=>6(-9x+9)=5(3x-2)
=>-54x+54=15x-10
=>-69x=-64
=>69x=64
=>\(x=\dfrac{64}{69}\)
l: ĐKXĐ: \(x\notin\left\{1;2\right\}\)
\(\dfrac{1}{x-1}-\dfrac{7}{x-2}=\dfrac{1}{\left(x-1\right)\left(2-x\right)}\)
=>\(\dfrac{x-2-7\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}=\dfrac{-1}{\left(x-1\right)\left(x-2\right)}\)
=>x-2-7(x-1)=-1
=>x-2-7x+7=-1
=>-6x+5=-1
=>-6x=-6
=>x=1(loại)
k: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{1}{x+1}+\dfrac{2}{x^3-x^2-x+1}=\dfrac{3}{1-x^2}\)
=>\(\dfrac{1}{x+1}+\dfrac{2}{x^2\left(x-1\right)-\left(x-1\right)}=\dfrac{-3}{\left(x-1\right)\left(x+1\right)}\)
=>\(\dfrac{1}{x+1}+\dfrac{2}{\left(x-1\right)^2\cdot\left(x+1\right)}=\dfrac{-3}{\left(x-1\right)\left(x+1\right)}\)
=>\(\dfrac{\left(x-1\right)^2+2}{\left(x+1\right)\left(x-1\right)^2}=\dfrac{-3\cdot\left(x-1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
=>\(\left(x-1\right)^2+2=-3\left(x-1\right)\)
=>\(x^2-2x+1+2+3x-3=0\)
=>\(x^2+x=0\)
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
j: ĐKXĐ: \(x\notin\left\{2;-1\right\}\)
\(\dfrac{x+10}{x^2-x-2}+\dfrac{3}{x+1}-\dfrac{2}{2-x}=1\)
=>\(\dfrac{x+10}{\left(x-2\right)\left(x+1\right)}+\dfrac{3}{x+1}+\dfrac{2}{x-2}=1\)
=>\(\dfrac{x+10+3\left(x-2\right)+2\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}=1\)
=>\(\dfrac{x+10+3x-6+2x+2}{\left(x-2\right)\left(x+1\right)}=1\)
=>\(\left(x-2\right)\left(x+1\right)=6x+6\)
=>(x-2)(x+1)-6(x+1)=0
=>(x+1)(x-8)=0
=>\(\left[{}\begin{matrix}x=-1\left(loại\right)\\x=8\left(nhận\right)\end{matrix}\right.\)
m: |2x+5|=6
=>\(\left[{}\begin{matrix}2x+5=6\\2x+5=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=1\\2x=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{11}{2}\end{matrix}\right.\)
n: |3x+1|=6-x
=>\(\left\{{}\begin{matrix}6-x>=0\\\left(3x+1\right)^2=\left(6-x\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =6\\\left(3x+1-6+x\right)\left(3x+1+6-x\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =6\\\left(4x-5\right)\left(2x+7\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{5}{4};-\dfrac{7}{2}\right\}\)
o: |5-2x|-4=x
=>|2x-5|=x+4
=>\(\left\{{}\begin{matrix}x+4>=0\\\left(2x-5\right)^2=\left(x+4\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-4\\\left(2x-5-x-4\right)\left(2x-5+x+4\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-4\\\left(x-9\right)\left(3x-1\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{9;\dfrac{1}{3}\right\}\)



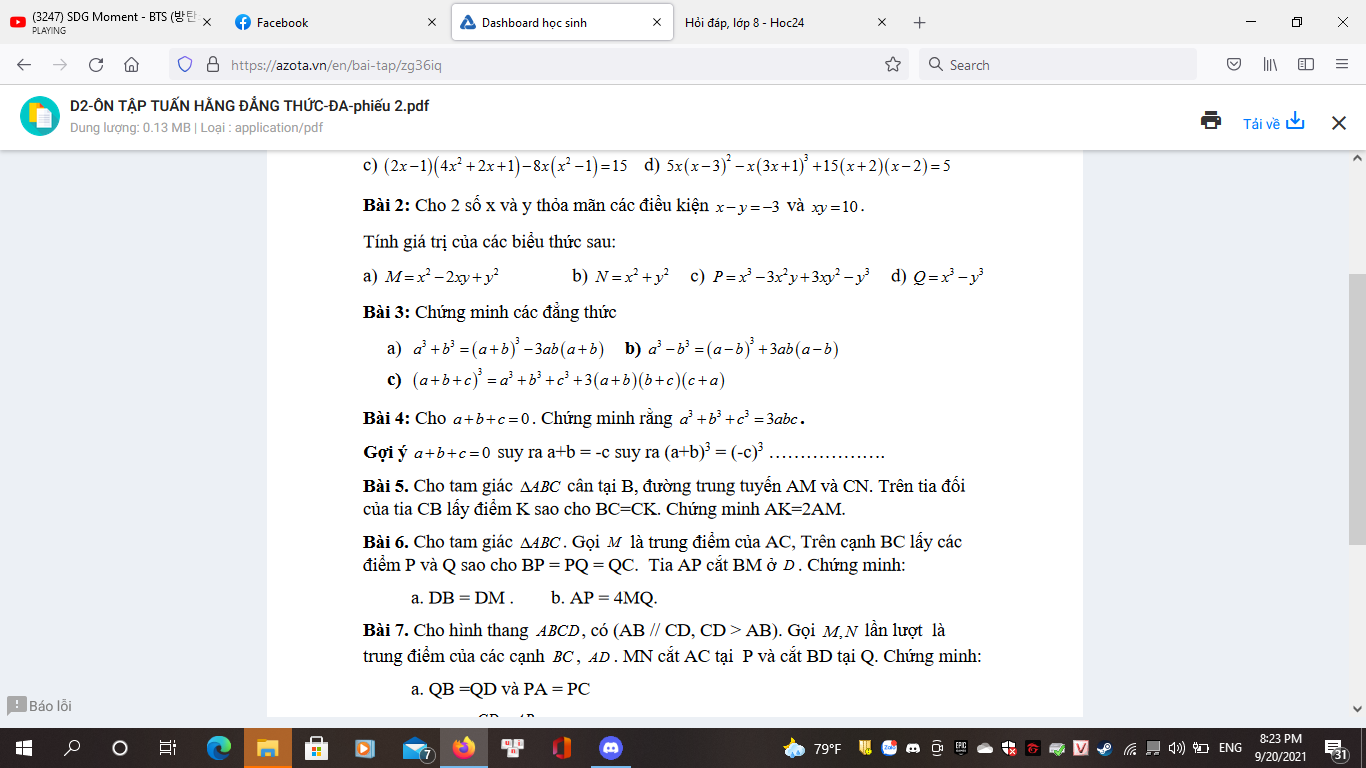 mng giúp mình bài 2 bài 3 bài 4 vs ah
mng giúp mình bài 2 bài 3 bài 4 vs ah
 ai giúp mình bài 2 vs =))))
ai giúp mình bài 2 vs =))))

