a) \(2^x.2^2=32\\ \Rightarrow2^{x+2}=2^6\\ \Rightarrow x+2=6\\ \Rightarrow x=4\)
b) \(27.3^x=243\\ \Rightarrow3^3.3^x=3^5\Rightarrow3^{3+x}=3^5\\ \Rightarrow3+x=5\\ \Rightarrow x=2\)
c) \(2^x.2^4=1024\\ \Rightarrow2^{x+4}=2^{10}\\ \Rightarrow x+4=10\\ \Rightarrow x=6\)
d) \(49.7^x=2401\\ \Rightarrow7^2.7^x=7^4\\ \Rightarrow7^{2+x}=7^4\\ \Rightarrow2+x=4\\ \Rightarrow x=2\)
j: Ta có: \(2^x+2^{x+4}=272\)
\(\Leftrightarrow2^x\cdot17=272\)
\(\Leftrightarrow2^x=16\)
hay x=4
h: Ta có: \(3x+23=5^6:5^3\)
\(\Leftrightarrow3x=125-23=102\)
hay x=34
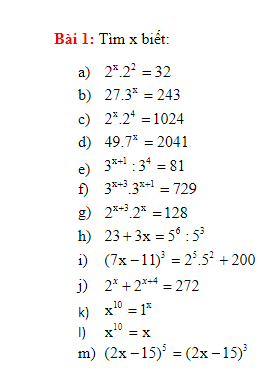 Giúp mik zới nha
Giúp mik zới nha


 Mấy bạn giúp mik lẹ zới , cho mik đáp án đầy đủ trong vòng 10phut nha , ( các bạn làm đc bài nào thì làm )
Mấy bạn giúp mik lẹ zới , cho mik đáp án đầy đủ trong vòng 10phut nha , ( các bạn làm đc bài nào thì làm ) 
