a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC=BC/2
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
b: ΔMAC cân tại M
mà MO là đường cao
nên O là trung điểm của AC
Xét tứ giác AMCN có
O là trung điểm chung của AC và MN
=>AMCN là hình bình hành
Hình bình hành AMCN có MA=MC
nên AMCN là hình thoi
c: Xét tứ giác MNCD có
I là trung điểm chung của MC và ND
=>MNCD là hình bình hành
=>MD//CN
Ta có: AMCN là hình thoi
=>CN//AM
mà MD//CN
và MD,MA có điểm chung là M
nên A,M,D thẳng hàng
d: Ta có: MDCN là hình bình hành
=>MD=CN
mà CN=MA
nên MD=MA
=>M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>BD//AC
mà MN\(\perp\)AC
nên NM\(\perp\)BD
Để M là trực tâm của ΔNBD thì DM\(\perp\)BN
=>AM\(\perp\)BN
Ta có: AN=MC
mà MC=MB
nên AN=MB
Xét tứ giác ANMB có
AN//MB
AN=MB
Do đó: ANMB là hình bình hành
Hình bình hành ANMB có AM\(\perp\)BN
nên ANMB là hình thoi
=>AB=BM
mà BM=MA
nên AB=MA=MB
=>ΔABM đều
=>\(\widehat{ABC}=60^0\)



 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều


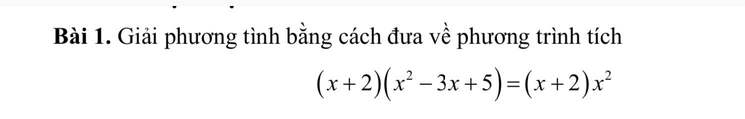


 giúp mik vs mik đag cần gấp
giúp mik vs mik đag cần gấp